Nonparametric regression is a very attractive method in practice because it is very flexible and has relatively loose restrictions on the prior structure assumptions of unknown regression functions. However, the corresponding cost is that it requires a large amount of labeled data, and it grows exponentially with the increase of dimensionality-the so-called curse of dimensionality. Annotating data is extremely time-consuming and labor-intensive, and in many scenarios, the acquisition of ordinal information is relatively inexpensive. In view of this, CMU researcher Yichong Xu et al. proposed a semi-supervised algorithm Ranking-Regression, which combines a small number of labeled samples with a large number of unlabeled samples to escape the curse of dimensionality.
Non-parametric method
In the supervised learning problem, we have some labeled data (observations), and then look for a function that can fit these data well.
Given some data points, to find a function that fits these data points, the first thing we think of is linear regression:
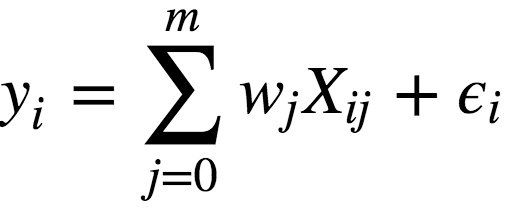
among them:
y is the dependent variable (ie target variable);
w is the parameter of the model;
X is the observation and its characteristic matrix;
ϵ is the variable corresponding to the random, unpredictable model error.
We can see that the process of linear regression is actually to find the parameter w that best fits the observation. Therefore, linear regression is a parametric method.
However, linear regression assumes that the linear model can fit the data well, which is not necessarily true. The relationship between many data is non-linear, and it is difficult to approximate the linear relationship. In this case, we need to use other models to better fit the data, such as polynomial regression.
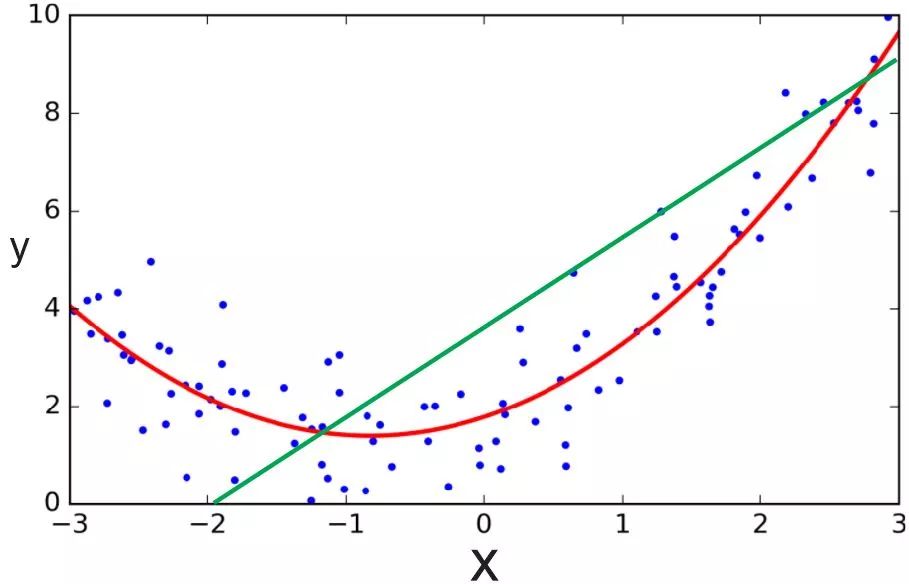
The green line is linear regression, and the red line is polynomial regression; image source: ardianumam.wordpress.com
Whether it is linear regression or polynomial regression, there are strong assumptions about the structure of the model in advance. For example, data can be fitted by linear or polynomial functions, but these assumptions are not necessarily true. Therefore, in many scenarios, we need to use non-parametric regression, that is, we not only need to find the parameters of the regression function, but also need to find the structure of the regression function.
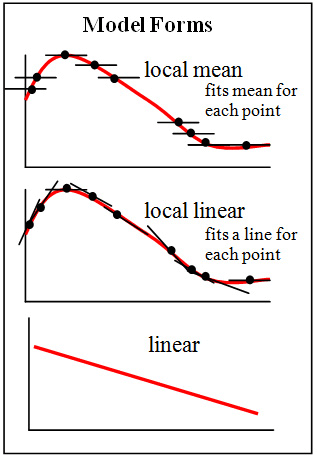
Image source: Brmccune; License: CC BY-SA 3.0
For example, the K nearest neighbor algorithm, which is usually used for classification, can actually be used for regression. The K-nearest neighbor algorithm used for regression has the same basic process as the general K-nearest neighbor algorithm for classification. The only difference is that the classification of the target variable is the most common classification (mode) among its nearest neighbors. In regression, the value of the target variable is the mean (or median) of its nearest neighbors. The K nearest neighbor algorithm used for regression is a non-parametric regression method.
Of course, the flexibility of non-parametric methods is not without cost. Since not only the parameters of the regression function are unknown, but the structure of the regression function is also unknown. Compared with the parameter method, we need more labeled data for training to get better results. As the dimensionality increases, the amount of labeled data we need increases exponentially. This is exactly the curse of the dimension we mentioned earlier. Earlier, we cited K-nearest neighbor as an example of nonlinear regression, and K-nearest neighbor is becoming famous because of the curse of dimensionality.
In view of this, many studies are devoted to alleviating this problem by adding structural constraints to non-parametric regression, for example, sparsity or manifold constraints (in many cases, high-dimensional data space is sparse, and sometimes high-dimensional data even Basically on a low-dimensional manifold). This is a very interesting thing. In practice, the reason for choosing non-parametric regression is to value its flexibility, and there is no strong assumption about the structure of the fitting function. However, when non-parametric regression encounters the curse of dimensionality, we take a step back and alleviate the curse of dimensionality by strengthening the structural assumptions.
The CMU researchers Yichong Xu, Hariank Muthakana, Sivaraman Balakrishnan, Aarti Singh, Artur Dubrawski took another approach, using a larger data set with ordinal information to supplement the smaller labeled data set, and alleviate the high level of non-parametric regression. The problem under the dimension. This approach is of great significance in practice, because the cost of collecting order information is much lower than that of labels. For example, in the clinic, it may be difficult to accurately assess the health of a single patient, but it is easier and more accurate to compare two patients who are healthier.
Sorted regression algorithm
The ranking regression (Ranking-Regression) algorithm (hereinafter referred to as R2) proposed by the researchers, its basic intuition is to infer the value of unlabeled data points based on the order information. Specifically, the data points are sorted according to ordinal information, and then isotonic regression is applied, and then the values ​​of unlabeled data points are inferred based on the labeled data points and the ordinal information. After the above process, the nearest neighbor algorithm can be used to estimate the value of the new data point.
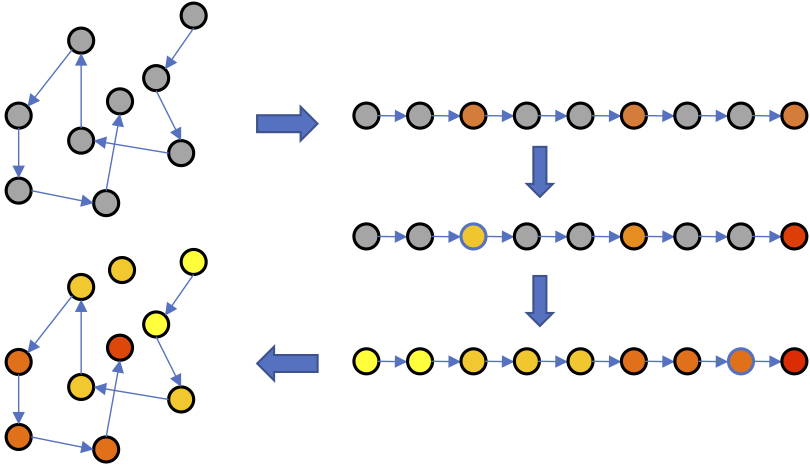
Algorithm diagram
The above is a schematic diagram of the R2 algorithm. Of course, if you are more accustomed to looking at pseudo code:

R2 upper and lower bounds
Obviously, substituting sequence information for labels is a quailty. Therefore, the researchers studied the upper and lower bounds of the error of the R2 algorithm.
As mentioned earlier, nonparametric regression has looser assumptions about structure, but it is not unlimited. The researchers used classic nonparametric regression restrictions:
In the unlabeled data set {X1, ..., Xn}, Xi ∈ X ⊂ [0,1]d, and Xi is uniformly and independently extracted from the distribution Px. And Px satisfies its density p(x) to be bounded for x ∈ [0,1]d, namely 0
The regression function f is also bounded ([-M, M]) and is Herder continuous at 0
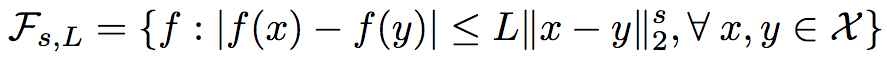
Under the condition that the above conditions are met, the researchers proved that the upper bound of the mean square error of the regression function obtained by R2 is:
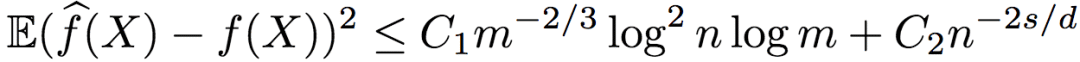
Among them, C1 and C2 are constants greater than zero.
The lower bound of the mean square error of the regression function is:
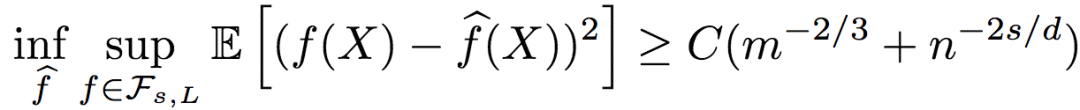
Among them, C is a constant greater than zero.
It can be seen from the upper and lower bounds of the error that the sorting regression based on ordinal information has a good effect, and it is optimal from the logarithmic factor.
In addition, from the upper bound of R2 error, only the order information (n) depends on the dimension d (the second term on the right side of the inequality), while the label information does not depend on the dimension d (the first term on the right side of the inequality), that is to say , R2 escaped the curse of dimensionality.
Due to space limitations, the proof process will not be introduced here. For the proof ideas of the upper and lower bounds, see Section 3.1 and Section 3.2 of the paper respectively; for the detailed proof process, see Appendix B and C of the paper respectively.
Noisy sequence information
Although it was said before that the order information is relatively easy to obtain and it is easier to maintain accuracy, but the actual data will inevitably have noise-wrong order information. The previous conclusions are all based on the premise that the sequence information does not contain noise. So, what happens when the sequence information is noisy?
The researchers further deduced that the order information contains noise. Of course, the noise is controlled within a certain range. Assuming that the Kendall-Tau distance between the sort obtained according to the noisy order information and the real order does not exceed vn2 (n represents unlabeled data with only order information), the upper bound of the mean square error of R2 is:
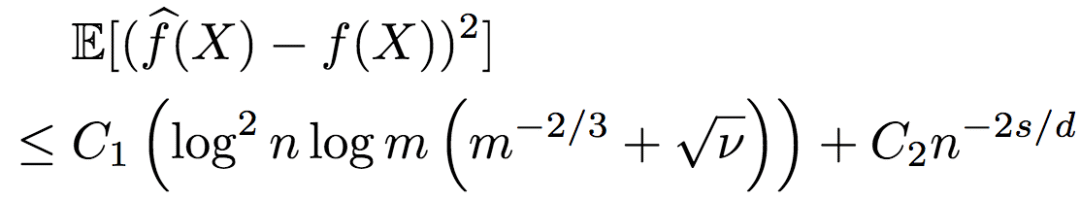
The lower bound is:
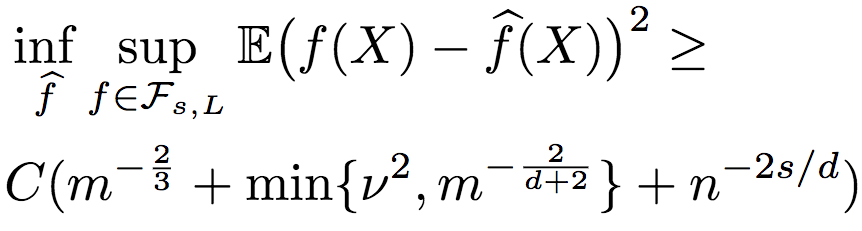
It can be seen that the robustness of R2 is quite good. When there is enough order information, even if the order information contains some noise, the labeled data still does not depend on the dimension, that is, R2 can still escape the curse of dimensionality.
Similarly, we will not give a specific proof process here. Please refer to sections 4.1 and 4.2 of the paper for the proof ideas, and Appendix D and F of the paper for the detailed proof process.
In addition, the researchers further proved (see Appendix E for the proof process) that there is an approximation function f that satisfies
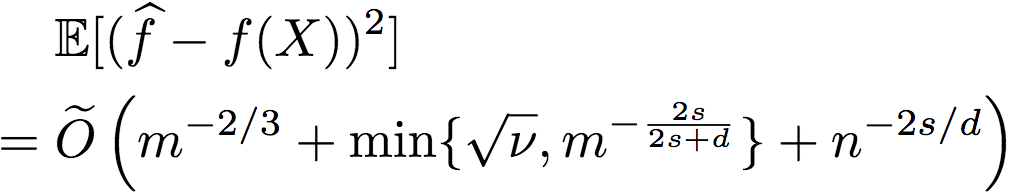
This means that when the noise is too large (v is too large), by using the cross-validation process (R2 and a simple non-parametric regressor that ignores the order information), we can choose a better regression method to achieve better performance . In fact, when we have enough labels, even if the order information is very noisy, the above ratio can still converge to 0.
Noisy paired comparison
Sometimes, the order information is obtained in the form of a pairwise comparison (the size between two data points). When there is no noise, the pairwise comparison is equivalent to the aforementioned standard sorting form. But the situation with noise is different. Researchers have proved that when the order information is pairwise comparison with noise, the upper bound of the mean square error of the approximation function is:
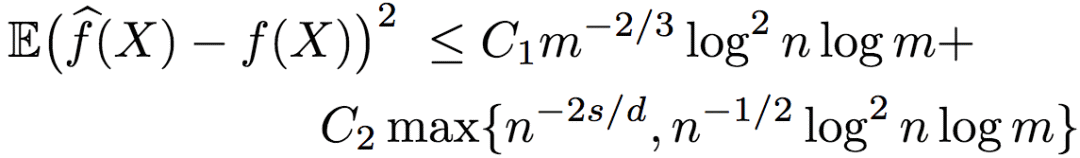
Among them, C1 and C2 are constants greater than zero.
It can be seen from the above formula that when the dimension d >= 4s, the error depends on n-2s/d, and, under this setting, the sorted regression based on noise-containing pairwise comparisons is also logarithmic factor optimal.
test
In order to verify the theoretical results and test the actual performance of R2, the researchers conducted some experiments:
Experiment on simulated data so that noise can be fully controlled
Experiment on the UCI data set and simulate sorting through tags
Test R2's performance in practical applications
In all experiments, the researchers compared the performance of R2 and K nearest neighbor algorithms. The K-nearest neighbor is chosen because K-nearest neighbor is close to optimal in theory and is widely used in practice. Theoretically, when there are m labeled samples, the optimal value of k is m2/(d+2). However, for all the values ​​of m and d considered by researchers, m2/(d+2) is very small (
Simulation data
The researchers used the following method to generate the data: Let d = 8, uniformly sample X from [0, 1]d. The objective function is:
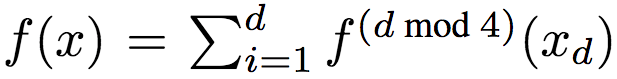
Where xd is the dth dimension of x, and
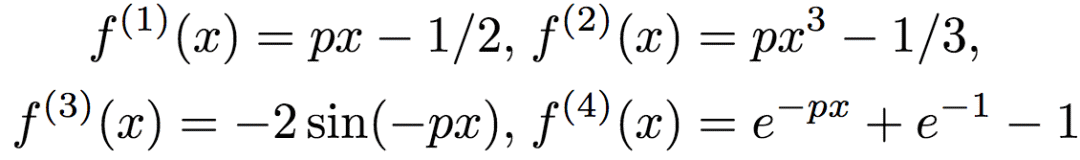
Among them, p is randomly and uniformly sampled from [0, 10]. The researchers adjusted f(x) so that its mean is 0 and the variance is unit variance. Generate labels by y = f(x) + ε, ε ~ N(0, 0.52).
The researchers generated 1,000 samples for the training set and test set.
The researchers tested two variants of R2, 1-NN and 5-NN, using 1 and 5 nearest neighbors respectively in the last step of the algorithm. 5-NN does not affect the upper and lower bounds of the previous theoretical analysis part. However, based on experience, researchers have found that 5-NN improves performance.
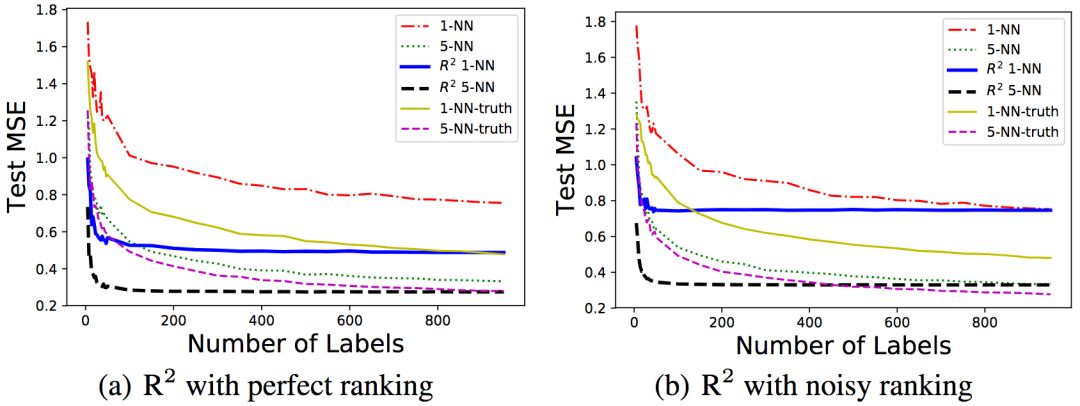
Left: Sequence information is noisy; Right: Sequence information is noisy
As can be seen from the above figure, regardless of whether the order information is noisy, R2 performs well.
In order to study the influence of order information noise, the researchers changed the level of order information noise while fixing the number of labeled/ranked samples at 100/1000. For the noise level σ, the order information is generated by y'= f(x) + ε', where ε'~ N(0, σ2).
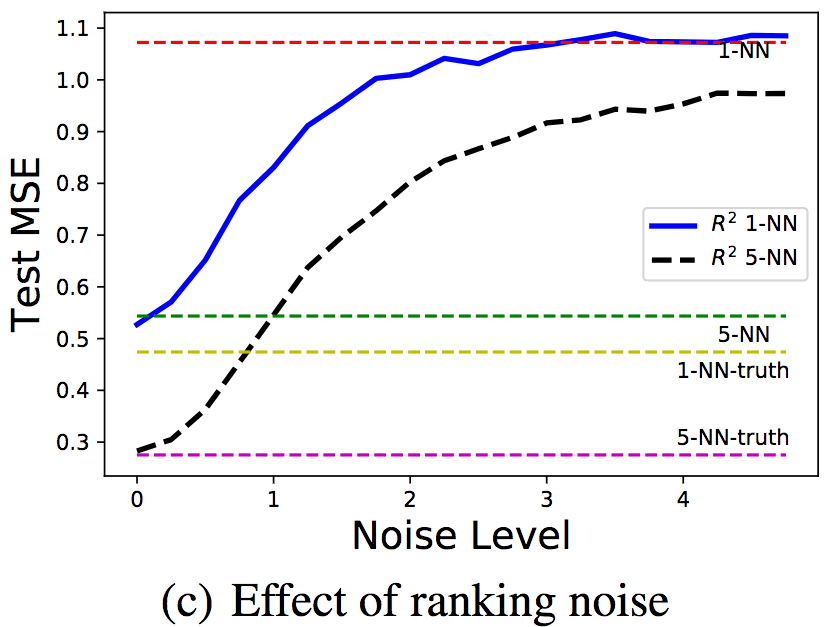
It can be seen that as the noise level increases, the mean square error increases accordingly.
UCI data set
The researchers conducted experiments on two UCI regression data sets. These two data sets are Boston-Housing (Boston housing prices) and diabetes (diabetes). The order information is generated by the data set label.
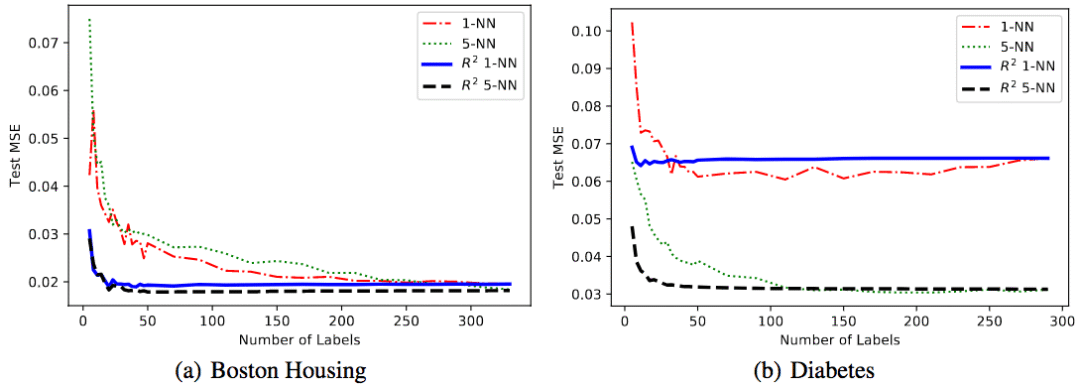
It can be seen that R2 performs better on both data sets compared to the baseline that does not use order information.
Predict age based on portrait
In order to further verify the R2 algorithm in practice, the researchers considered the task of estimating the age of a person based on a portrait.
The researchers used the APPA-REAL dataset, which contains 7,591 images, each with a corresponding biological age and apparent age. The biological age is the actual age, and the apparent age is based on crowdsourced collection. Obtain the apparent age based on the average of multiple estimates (there are 38 different estimators on average). APPA-REAL also provides the standard deviation of the apparent age estimate. The data set is divided into three parts, 4113 training images, 1500 verification images, and 1978 test images. The researchers' experiments only used training and verification samples.
The researchers used the last layer of FaceNet to extract 128-dimensional features from each image, and scaled each feature so that each sample X ∈ [0, 1]d. The researchers used 5-NN and 10-NN. In addition to using 5-NN and 10-NN that do not contain order information as baselines, as in previous experiments, the performance of kernel support vector regression (SVR) was also compared. The parameter configuration of SVR is the standard configuration of scikit-learn, the penalty parameter C = 1, the RBF core, and the tolerance value is 0.1.
The researchers tested two tasks:
The goal of the first task is to predict biological age. The label is the biological age, and the order information is generated based on the apparent age. This is to simulate a real scene, with a small sample of real age information, but hope to collect more samples of age information through crowdsourcing. In crowdsourcing, it is easier and more accurate for people to sort the sample's age than to directly estimate the age.
The goal of the second task is to predict the apparent age. In this task, labels and rankings are generated based on the standard deviation provided by APPA-REAL. Specifically, the label is sampled from a Gaussian distribution, the mean is equal to the apparent age, and the standard deviation is the standard deviation provided by the data set. The sorting is generated in two steps. First, labels are generated according to the same distribution, and then sorted according to the labels. This is to simulate the real scene, let people estimate the age of the sample at the same time, and sort the age of the sample. Note that in real applications, compared to experiments, the sorting noise will be lower.
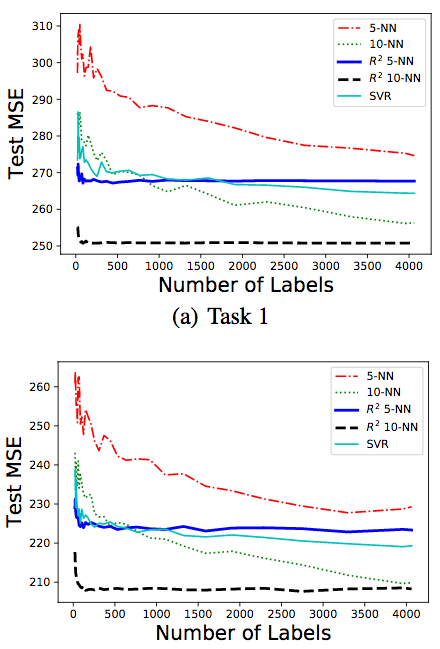
The result is shown in the figure above. We can see that the 10-NN version of R2 performs best. When the number of samples is less than 500, the 10-NN version and 5-NN version of R2 are better than other algorithms.
Conclusion
Papers can be obtained through the preprinted text library: arXiv:1806.03286
In addition, the author of this article will give an oral report on ICML 2018 (Wed Jul 11th 11:00 - 11:20 AM @ A6).
The 8-inch tablet will have a big impact on the 7-inch and 10-inch tablet market. Because the portability of an 8-inch tablet is stronger than that of a 10-inch tablet, and the usable area is larger than that of a 7-inch tablet. The most important thing is that the price is more moderate, which is much cheaper than a 10-inch tablet. It can be said that the 8-inch tablet computer has a good balance between portability and screen display area, and is more likely to be favored by the majority of users.
8 Inches Tablet Pc,Tablet Computer,8 Inch Android Tablets,8 Inch Tablet
Jingjiang Gisen Technology Co.,Ltd , https://www.jsgisengroup.com