Lei Feng network (search "Lei Feng network" public number concerned) : Author of this article Guo Qing, Liu Wei. The article talks about artificial neural networks from neural networks and introduces them in detail.
The recent "neural network" is very hot, especially after the game between AlphaGo and South Korea's Li Shishi ended. Various articles about neural networks are flying all over the world, but it may be that people who come from non-professional backgrounds will get into trouble with these articles. . The main reason is that there is a lack of popular science articles that suit most people's understanding of neural networks. In fact, Wu Jun's “Mathematical Beauty†is more straightforward to understand in the popular science neural network. Interested friends can read Miss Wu. book of. This article is different from Wu's explanation method. The author hopes to uncover the veil of the neural network from the origin of the neural network, thereby helping more friends interested in the neural network but no relevant theoretical basis.
Speaking of the origin of artificial neural networks must be traced back to biological neural networks. Here we look at a video on the principle of neuronal cells:
Http://Qi_LbKp7Kk/VUQGmBXIzf0.html
To sum up, the neurons are composed of a cell body, some dendrites, an axon, and many synapses. The neuronal cell body is the main body of a neuron and contains nuclei. Dendrites extend from the cell body to a number of nerve fibers that are used to receive input signals from other neurons. Axons send out signals through the branching nerve endings and contact the dendrites of other nerve cells to form so-called synapses. The following figure is neuron cells in the human brain. Everyone can understand the neuron cell map and understand it.
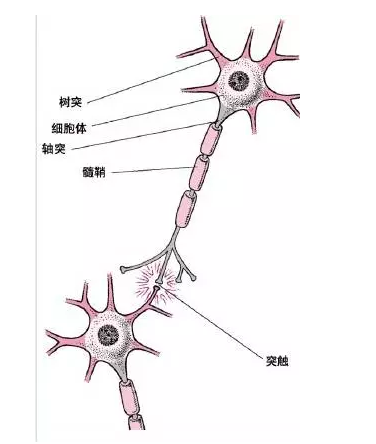
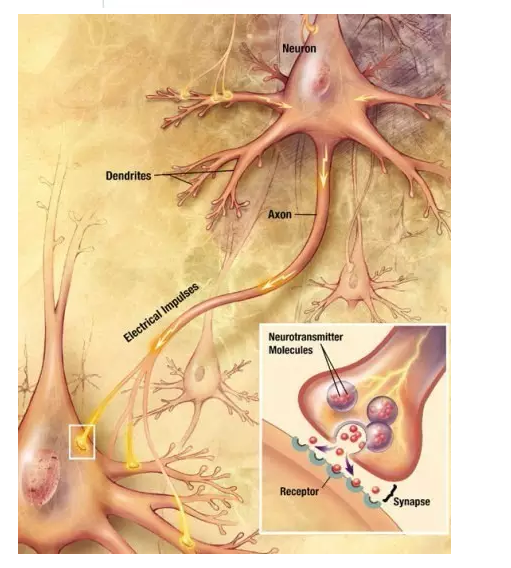
In order to facilitate the understanding of the artificial neural network, we hereby summarize the characteristics of the important components of neuronal cells:
1. Dendrites, axons, and synapses correspond to the input, output, and input/output interfaces (I/O) of the cell body, respectively, and are multi-input and single-output.
Excitatory and inhibitory synapses determine neuronal excitation and inhibition (corresponding to the frequency of the output bursts, respectively), where the bursts represent neuronal information;
3. Pulses are generated when the potential difference between the inner and outer cell membranes (the sum of synaptic input signals) exceeds the threshold, and the nerve cells enter the excited state;
4. Synaptic delay causes a fixed time lag between input and output.
Artificial neural networks
In 1943, the McCulloch-Pitts' neuron model was born based on the biological neural network. It was co-sponsored by psychologist Warren McCulloch (pictured left) and mathematician Walter Pitts (pictured right).

The basic idea of ​​the McCulloch-Pitts model is to abstract and simplify the characteristic components of biological neurons. This model does not need to capture all the properties and behavior of a neuron, but it is sufficient to capture the way it performs calculations. In the six features of the McCulloch-Pitts model, the first four points are the same as the biological neurons summarized before. See the figure below for details:
1. Each neuron is a multi-input single-output information processing unit;
2. There are two types of neuronal input: excitatory input and inhibitory input;
3. Neurons have spatial integration characteristics and threshold characteristics;
4. There is a fixed time lag between neuron input and output, which mainly depends on synaptic delay;
5. Ignore time integration and refractory period;
6. The neurons themselves are not time-varying, ie their synaptic delays and synaptic strengths are constant.
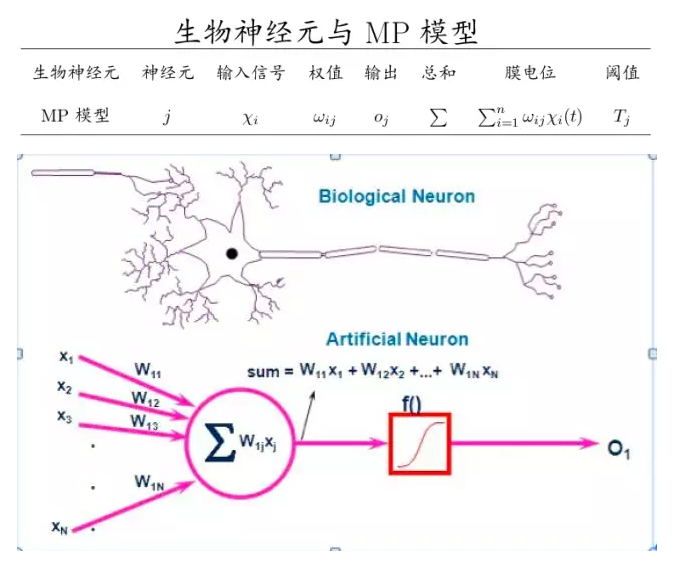
The McCulloch-Pitts model formula is as follows:
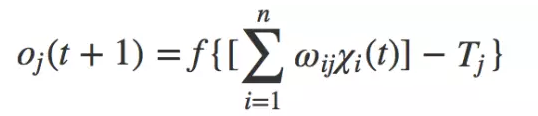
The operating rule is: the time is discrete, and the excitatory input xi is obtained at time t (t=0,1,2,...). If the membrane potential is equal to or greater than the threshold and the inhibitory input is 0, at time t+1, the neuron cell The output is 1 otherwise it is 0.
This great modeling is no exception. Dividing the colors and shapes into two categories from the human point of view requires only eye discrimination, but for machines it can discern just a bunch of data. If there are two sets of data on the plane (as shown below), how does the machine distinguish between the two sets of data? There are two types of data that can be divided into two types by the linear equation on the plane. The artificial nerves constructed by Warren McCulloch and Walter Pitts Yuan is such a model. Its essence is to take all two parts of the feature space and consider that the two halves belong to two classes. You may not even think of a simpler classifier than this.
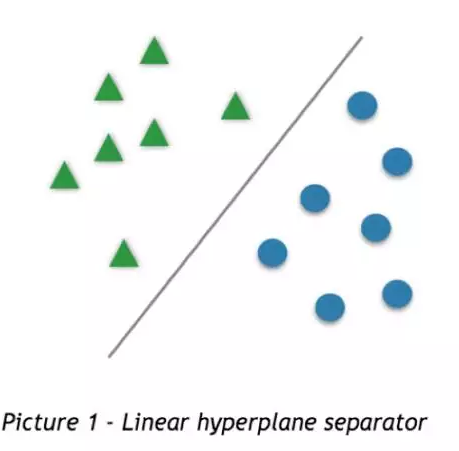
However, the McCulloch-Pitts model lacks a learning mechanism that is critical to artificial intelligence. Therefore, here we need to popularize "history" for everyone. In 1949, Donald Hebb stated that knowledge and learning occurred in the brain mainly through the formation and changes of synapses between neurons. This unexpected and far-reaching idea was abbreviated as Heb'Fah:
When the axons of cell A are close enough to stimulate cell B and repeatedly discharge cell B repeatedly, some growth process or metabolic changes will occur in one or both of these cells, so that A acts as a cell that discharges to B An increase in efficiency.
In the popular sense, the more two neurons communicate, the higher the efficiency of their connection, and vice versa. Frank Rosenblatt was inspired by the basic work of Heb. In 1957 he proposed Perceptron. This is the first algorithm to precisely define a neural network. A sensor consists of two layers of neurons. The input layer receives signals from the outside world. The output layer is a McCulloch-Pitts neuron, which is a threshold logic unit.
In 1969, Marvin Minsky and Seymour Papert published a new book, Perception: An Introduction to Computational Geometry. The book demonstrates two key issues of the perceptron model: First, a single-layer neural network cannot solve the problem of non-linear segmentation. A typical example is like or (XNOR, if two inputs are the same, the output is 1; two inputs if The difference is that the output is 0.) Second, due to hardware level limitations, the computer at that time was completely unable to complete the huge amount of computation required by the neural network model.
Here, the author uses a single-layer neuron as an example to explain how artificial neurons work.
(We would like to thank the author of this site for providing English articles:
Http://)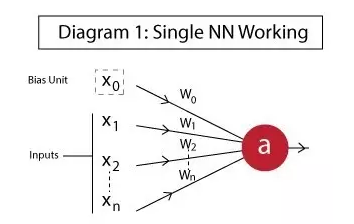
X1,x2,..., xN: input of neurons. These can be actually observed from the input layer or are a hidden layer of intermediate values ​​(hidden layer is a layer consisting of all the nodes between the input and output. Help the neural network to learn the complex relationship between data. We do not understand it does not matter, behind Speaking of multi-layer neural networks will be explained again.
X0: Offset unit. This is the input to which the constant value is added to the activation function (in a mathematical analogy y=ax+b is the constant b that makes the straight line not the origin). Intercept items, which usually have a +1 value.
W0,w1,w2,...,wN: The weight for each input. Even the bias unit is weighty.
a: output of neurons. Calculated as follows:
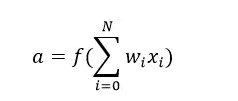
What needs to be explained is that f in the formula is a known activation function, f makes the neural network (single or even multi-layer) very flexible and has the ability to estimate complex nonlinear relationships. In the simple case it can be a Gaussian function, a logic function, a hyperbolic function or even a linear function. Using a neural network allows it to implement three basic functions: AND, OR, NOT.
Here's a basic f function, which is actually a step function we know well:
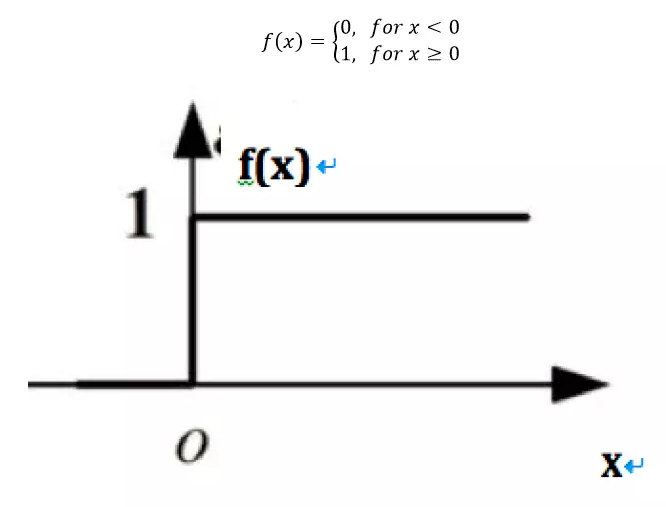
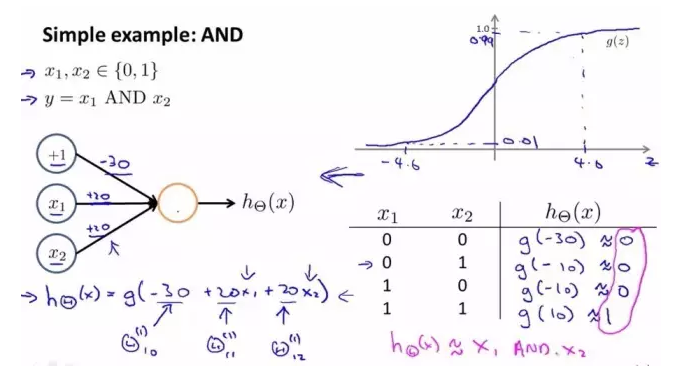
Example 1: The and function is implemented as follows:
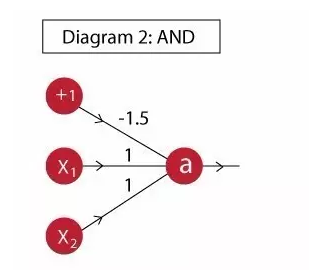
Neuron output: a = f ( -1.5 + x1 + x2 )
The truth table is as follows. It can be seen that the column "a" is consistent with the column "X1 AND X2":

Example 2: The or function is implemented as follows:
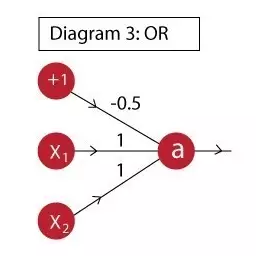
The neuron output is:
a = f(-0.5 + x1 + x2 )
The truth table is as follows, where column "a" is consistent with "X1 OR X2":

We can see from Example 1 and Example 2 that we can implement the or function by simply changing the weight of the bias unit. If either one of x1 or x2 is positive, the total weight is positive.
Example 3: The not function is implemented as follows:
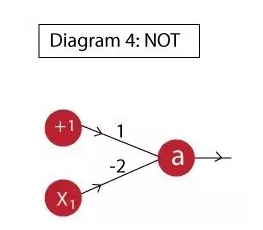
The neuron output is: a = f( 1 - 2 x1 )
The truth table is as follows:

The author hopes that through these examples we can intuitively understand how a neuron works in a neural network. Of course, there are multiple choices of functions in the neural network. In addition to the functions used in the above examples, here we introduce a commonly used function - sigmoid function, to help everyone understand. The function image looks like this:
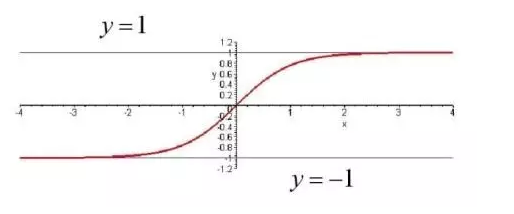
It can be seen from the figure that the advantage of the sigmoid function is that the output range is limited, so the data is not easy to divergence during the transfer process, and its output range is (0, 1), and the probability can be represented at the output layer. Of course, it also has the corresponding disadvantage, that is, the gradient is too small when saturated. We can understand the following and examples.
In the example we saw earlier, the AND, OR, and non-functions are linearly separable. The perceptron only has the output layer neurons to perform the activation function processing, ie it has only one layer of functional neurons and the learning ability is very limited (this is before this article One of the key issues in the perceptron model mentioned). Therefore, it is necessary to use multi-layer neurons for nonlinear separability. The following section introduces the multi-layer neural network.
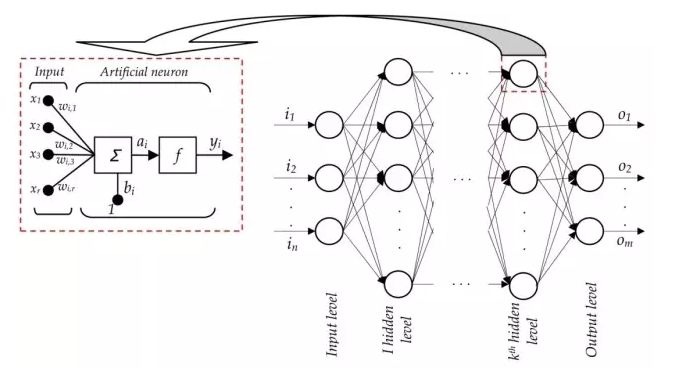
Neural networks are divided into three types of layers:
Input layer: The leftmost layer of the neural network through which the samples that need to be trained to observe are input.
Hidden layer: A layer consisting of all nodes between input and output. Helps neural networks learn complex relationships among data.
Output layer: The first layer of the neural network is obtained from the first two layers. In the case of 5 classifications, the output layer will have 5 neurons.
Why is a multi-layered network useful? Here we try to understand how neural networks use multi-layer to simulate complex relationships. To understand this further, we need to give an example of the same or a function. The truth table is as follows:
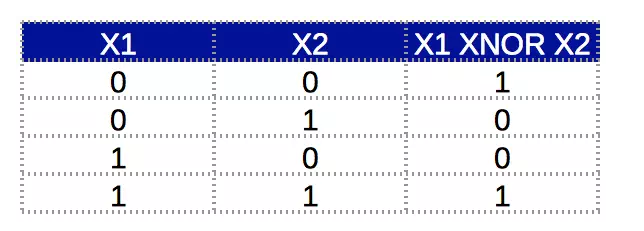
Here we can see that when the input is the same, the output is 1, and otherwise it is 0. This relationship cannot be completed by a single neuron and therefore requires a multi-layered network. The idea behind using multiple layers is that the complex relationship function can be broken down into simple functions and their combinations. Let us decompose the same or function:
X1 XNOR X2 = NOT (X1 XOR X2 )
= NOT [(A+B).(A'+B') ]
= (A+B)'+ (A'+B')'
=(A'.B') + (AB)
(Note: The symbol "+" here stands for or, the symbol "." stands for and the symbol "'" "-" stands for non.)
So we can use the simple example explained earlier.
Method 1: X1 XNOR X2 = (A'.B') + (AB)
Designing neurons to simulate A'.B' is a challenge that can be achieved by:
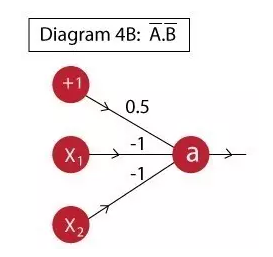
Neuron output: a = f( 0.5 – x1 – x2 )
The truth table is:
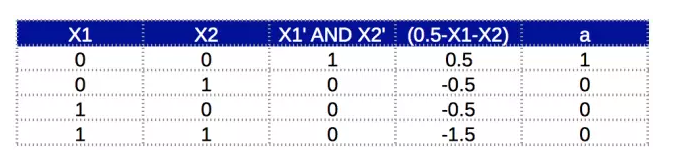
Now, everyone can treat A'.B' and AB separately as two separate parts and combine them into a multi-layered network. The semantic diagram of the network is as follows:
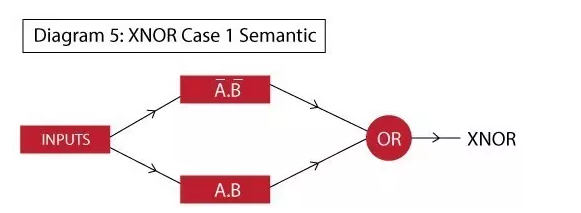
Here we can see that on the first level, we determine A'.B' and AB respectively. At the second level, we will output and implement the OR function at the top. The final overall network implementation is shown in the following figure:
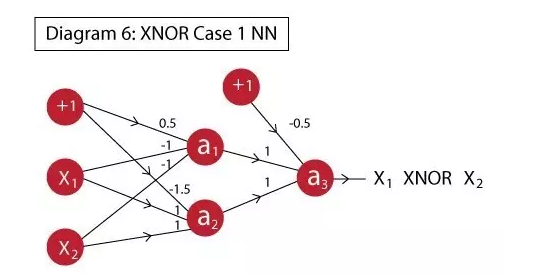
If you look closely, you will find that this is just a combination of the neurons we previously painted:
A1: achieved A'.B';
A2: Achieved AB;
A3: Establish OR on a1 and a2 to achieve an efficient implementation (A'.B' + AB).
Verify its functionality through a truth table:
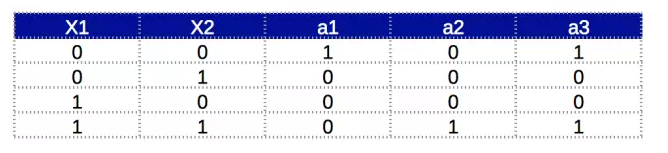
Now everyone should probably understand intuitively how multi-layer networks work. In the above example, we had to calculate A'.B' and AB separately. If we want to simply implement the same or a function based on the basic AND, OR, and NOT functions, we look at method 2 below.
Method 2: X1 XNOR X2 = NOT[ (A+B).(A'+B') ]
Here we use the formula obtained in the second step of the previous decomposition to achieve, the network semantics are as follows:
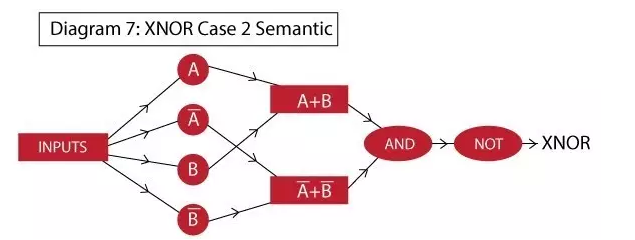
Everyone can see that neural networks have to use three hidden layers here. The overall network implementation is similar to what we did before:
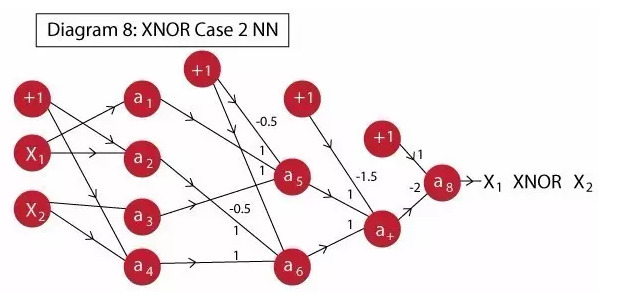
A1: Equivalent to A;
A2: A';
A3: Equivalent to B;
A4: Achieved B';
A5: Achieved OR, actually A+B;
A6: The OR is implemented, which is actually A'+B';
A7: AND is implemented, which is actually (A+B). (A'+B');
A8: NOT is implemented, actually NOT [(A+B).(A'+B')], which is the final XNOR output
The truth table is as follows:

Note: A typical neuron (except the bias unit) provides data for each neuron in the next layer. In this case, we have avoided several connections from the first layer to the second layer because their weight is 0, and adding them easily affects everyone's clear understanding of the calculations between neurons. So here is not drawn as below:
It can be seen that method 2 we have successfully achieved the same or a function. The idea of ​​method 2 is how to break a complex function into multiple layers. However, this method is more complicated than Method 1, so everyone should prefer Method 1.
Before I learned neural network, I also read a lot of information, and some of the information was in the cloud. The author hopes that after reading this article, we can avoid detours and understand neural networks. In the end, I quoted Wu's book and concluded by saying: “There are a lot of technical terms that make you very awkward. The 'artificial neural network' belongs to this category, and at least the first time I heard the word was stunned. You think, in people’s minds, people’s brain structure is still not clear at all, and this leads to an “artificial†neural network that seems to be using a computer to simulate the human brain. The structure is so complicated that everyone's first reaction must be that the artificial neural network must be very advanced.If we are fortunate enough to meet a kindly and articulate scientist or professor, he is willing to spend an hour or two and put the artificial neural network in the simplest way. The bottom line tells you that you will find, 'Oh, it turned out to be this.' If we unfortunately come across a lover, he will tell you solemnly, 'I am using artificial neural networks' or 'I study The topic of the problem is artificial neural networks, and then there is no such thing as following. In this way, in addition to respecting him, you cannot help but feel inferiority. Of course there is good intention but it is not good at expressing. People tried to make this concept clear to you, but he used some more ugly terms to talk about Yunshan Mist. Finally, you found that listening to him for several hours, the result was even more confusing. You lost nothing but wasted time. You come to a conclusion: In any case, I don't need to understand it in my life.
Don't think that I was joking. These are my personal experiences. First of all, I have not met the good people who have spoken to me in an hour or two. Next, I met a group of people who showed off in front of me. As young people, I always wanted to understand what I didn’t understand, so I decided Go to attend a class. However, after listening to it for about two or three times, I stopped going because because it was a waste of time, I didn't seem to get anything. Fortunately, I did not use it for the time being, and I no longer care. Later, during my doctoral studies in the United States, I like to read books before going to bed. I just hold a few textbooks about artificial neural networks on the bed and I actually read them. Then use it to do two or three projects, be regarded as learned. At this point, looking back at the 'Artificial Neural Network' is actually not complicated. It is not difficult to get started. I just went the wrong way.
Lei Feng Net Note: This article is authorized by the bright wind Taiwan Lei Feng network release, if you need to reprint please contact the original author.

Lynx Box M13
Installation Guide>>
Huawei Glory Box Pro
Installation Guide>>
Millet box 3
Installation Guide>>
Infinik i9
Installation Guide>>
KKTV
Installation Guide>>
Letv TV S50 Air
Installation Guide>> More than one stroke of the new Sharp PCI white matrix to create quality of life to create the history of the most fire 51, TCL air conditioning iron powder carnival crazy crazy eye-catching 51, TCL refrigerator washing machine first to buy Samsung to reduce Apple OLED screen supply: domestic machine spring coming? Can I use a TV as a monitor? Specific analysis and solution
More than one stroke of the new Sharp PCI white matrix to create quality of life to create the history of the most fire 51, TCL air conditioning iron powder carnival crazy crazy eye-catching 51, TCL refrigerator washing machine first to buy Samsung to reduce Apple OLED screen supply: domestic machine spring coming? Can I use a TV as a monitor? Specific analysis and solution  Three methods to teach you how to install live TV software for smart TV Samsung smart TV download software tutorial exclusive sofa butler international version of the cumulative 10 million downloads, cultivated overseas reputation for many years bursting How to watch live broadcast box? 80% smart TV and TV box are the best way to apply! When did the Extreme Challenge Fourth Season start on TV?
Three methods to teach you how to install live TV software for smart TV Samsung smart TV download software tutorial exclusive sofa butler international version of the cumulative 10 million downloads, cultivated overseas reputation for many years bursting How to watch live broadcast box? 80% smart TV and TV box are the best way to apply! When did the Extreme Challenge Fourth Season start on TV? 

