Research on Bistatic SAR Large Oblique Angle Imaging Algorithm Based on GPS
A GPS-based SAR system model was established. By equating the GPS signal to a Chirp signal, the large oblique viewing angle Chirp Scaling algorithm in this mode was studied. The CS algorithm has better focusing performance and wide applicability in the case of frontal or small squint, but in the case of a large slant angle of view, the algorithm will be out of focus and cannot be imaged, so an equivalent The single-base distance model replaces the bi-base distance history method, which solves the problem of large second-order approximation error of the distance model in the case of large oblique viewing angles, and combines the single-base nonlinear CS algorithm to achieve the High-precision bistatic SAR imaging of GPS reflected signals was finally verified by Matlab simulation.
Keywords: GPS; Bistatic Synthetic Aperture Radar; Track Mode; Large Oblique Angle; Nonlinear CS Algorithm
0 Introduction Passive SAR imaging systems based on GPS reflected signals are receiving more and more attention because of their superior performance and strong military and civilian development potential. Masters D and others used the GPS signals reflected on the ground to realize the measurement of the ground humidity; Garrison JL and others established a system model for extracting the state of the sea surface based on the GPS signals reflected by the sea surface, and conducted corresponding experiments to verify the effectiveness of this model. Lowe ST uses reflected GPS signals received from low-altitude aircraft to monitor changes in sea wave height. Studies have shown that GPS-based SAR imaging systems are completely feasible.
This paper studies the imaging system in the track mode. The so-called follow-track refers to the configuration mode of the GPS transmitter and receiver being separated forward and backward on the same movement trajectory and moving at the same speed and uniform speed. This mode formation formation is simple and easy to implement. At present, the Chirp Scaling algorithm is considered to be a more effective algorithm for this system. However, the original CS algorithm did not take into account the spatial variability of the slant range from the frequency of the spectrum spectrum, so it only accurately compensated the distance compression of the point target at the reference distance, and approximately compensated the point target at other distances. There will be defocusing. The NCS algorithm takes into account the space-variant characteristics of the distance spectrum modulation frequency, which greatly improves the processing capacity of squint data. However, the NCS algorithm requires a second-order expansion approximation of the distance history. Since the distance history of the bistatic base is the receiver, the transmitter to the target The distance sum is expressed as the sum of two square roots. If the second-order Taylor expansion method is still used, the error will be so large that it will affect the quality of imaging. This paper proposes an equivalent single-base distance model, which equates the history of the distance between two bases to a single base, which greatly reduces this error.
1 The signal model gives the geometric relationship of bistatic SAR in orbital flight mode as shown in Figure 1. In a short period of time, the GPS satellite and receiver move in a straight line at a constant speed along the route, and the closest vertical slope of the point target P For RB, suppose the time when the transmitter is at point o as the starting point of the slow time, at this time the beam rays can just hit the point target P, the transmitter is at point A, and the receiver is at point B, the transmitter and receiver beam The center points to a point target. After tm, the transmitter moves to A1 and the receiver moves to B1.
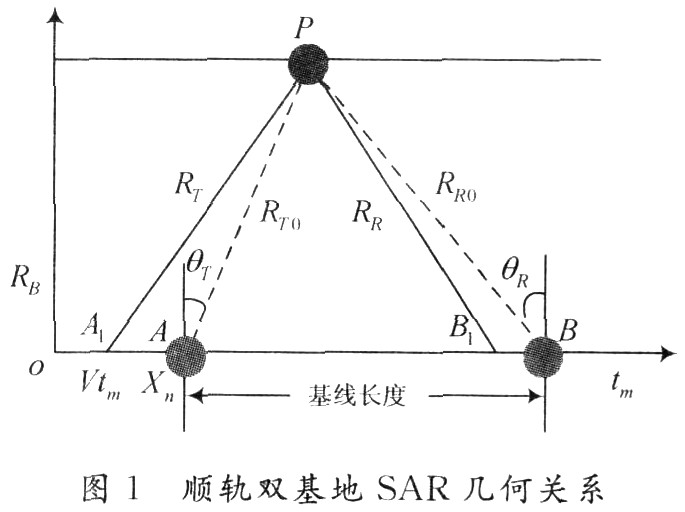
Through the above geometric relationship, the distance from the transmitter to the target can be calculated as:

Among them: RT0 = RB / cosθT, RR0 = RB / cosθR are the center slope distance from the transmitter and the receiver to the target respectively; given the baseline TR D, slope distance RB and transmitter observation angle θT, the receiver slope can be calculated Viewing angle θR = tan-1 (tanθT-TR D / RB). The echo model is determined by the transmitter model. When the transmitter oblique angle and the baseline between the transmitter and receiver are fixed, the receiver model is determined.
Based on the above analysis, the distance history of the echo transmitted from the transmitter to the receiver can be expressed as:
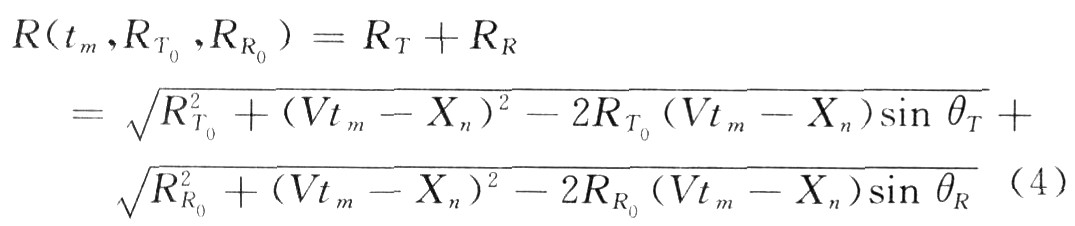
2 Equivalent single-base distance model
The GPS signal can be equivalent to a linear frequency modulation signal. After the point target echo is demodulated, the bistatic SAR echo signal can be expressed as:
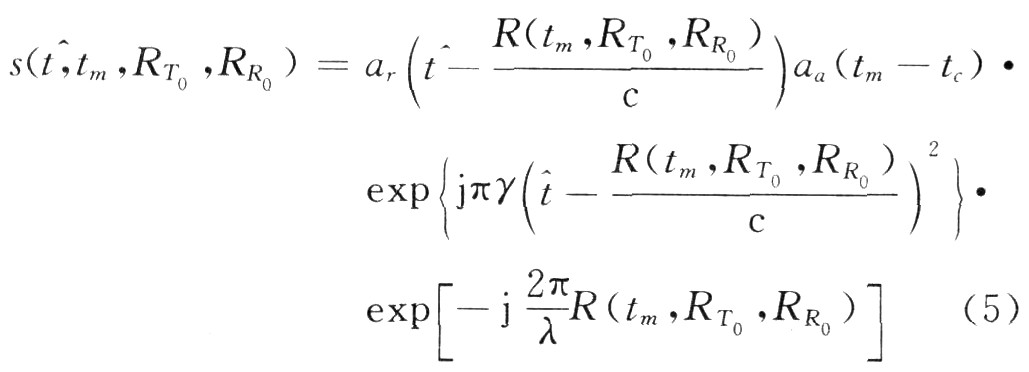
When performing imaging processing, it is necessary to derive the two-dimensional spectrum of the echo. When using the dwell phase principle to derive the two-bit spectrum of the echo in equation (5), it is difficult to directly find out because the distance history of the target is the sum of the two root formulas. The azimuthal dwell phase point, so the distance history of bistatic SAR can be considered to be equivalent to the unistatic SAR distance model, so that the two-dimensional spectrum of the echo can be easily derived.
When bi-base SAR is equivalent to single-base SAR, the distance history of equation (4) can be equivalent to:

Among them: R0 is the equivalent slant distance; θ is the equivalent oblique viewing angle; V0 is the equivalent speed. In order to calculate the equivalent parameters, formula (6) is expanded by Taylor series, and the first three coefficients are equal to obtain:
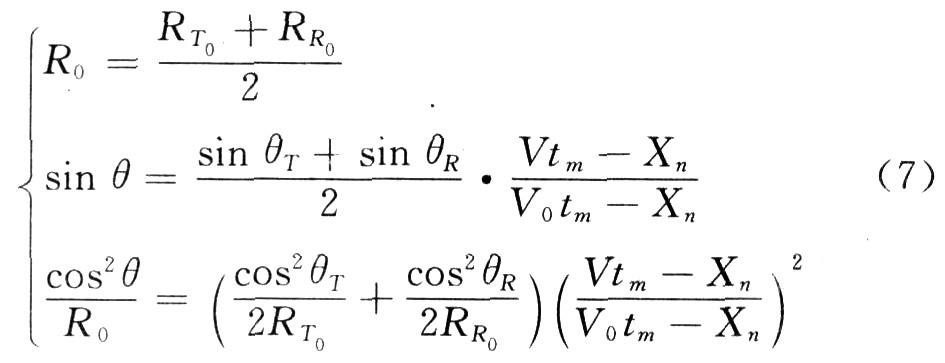
If the target position Xn is considered to be at the zero position, equation (7) can be simplified, and the equivalent parameters can be obtained by solving the equation:
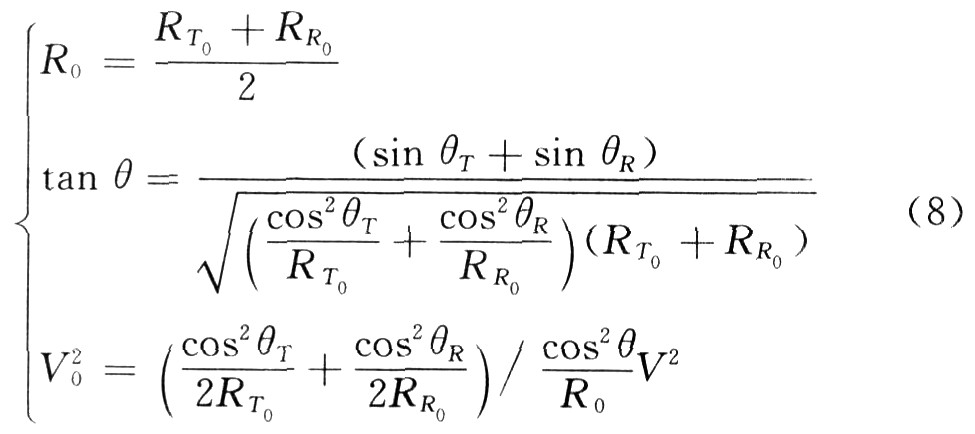
The bistatic SAR is calibrated into a single-base SAR with an oblique viewing angle of θ, a target slant range of R0, and a velocity of V0. At this time, the commonly used algorithms of single-base SAR can be used for imaging processing.
3 Squint NCS imaging algorithm According to the analysis, the equivalent single-base distance model can be used to replace the distance history of the bistatic SAR, so that the bistatic SAR imaging at a large oblique viewing angle is converted into the data processing of the monostatic strabismic SAR. Literature [5] studied the NCS algorithm in the case of large strabismus. Here, in combination with the above equivalent model, reference to this algorithm is used to image the bistatic SAR. The algorithm flow is shown in Figure 2. The specific form of each matching function is detailed below discussion.
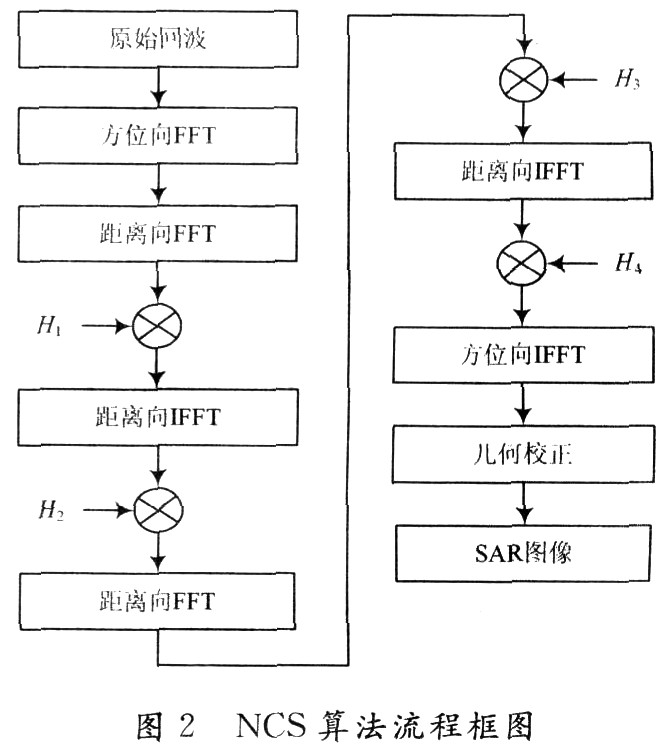
(1) Bistatic SAR echo signal The echo signal of the bistatic SAR is shown in equation (5). After the bistatic SAR is equivalent to the processing of the monostatic SAR, the approximated monostatic SAR signal form can be obtained, such as Formula (9) shows:
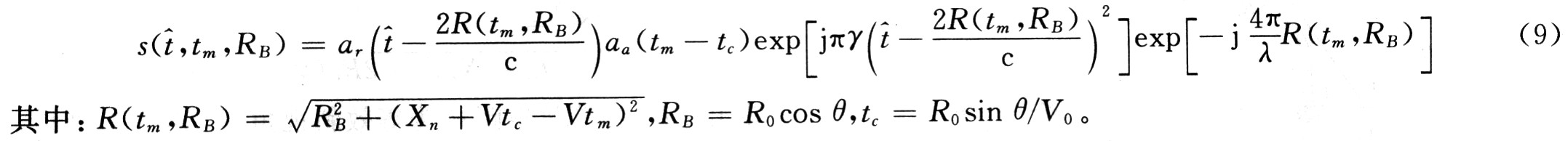
(2) Transform the echo into the two-dimensional frequency domain. Using the dwell phase principle, transform equation (9) into the two-bit frequency domain, which can be expressed as:
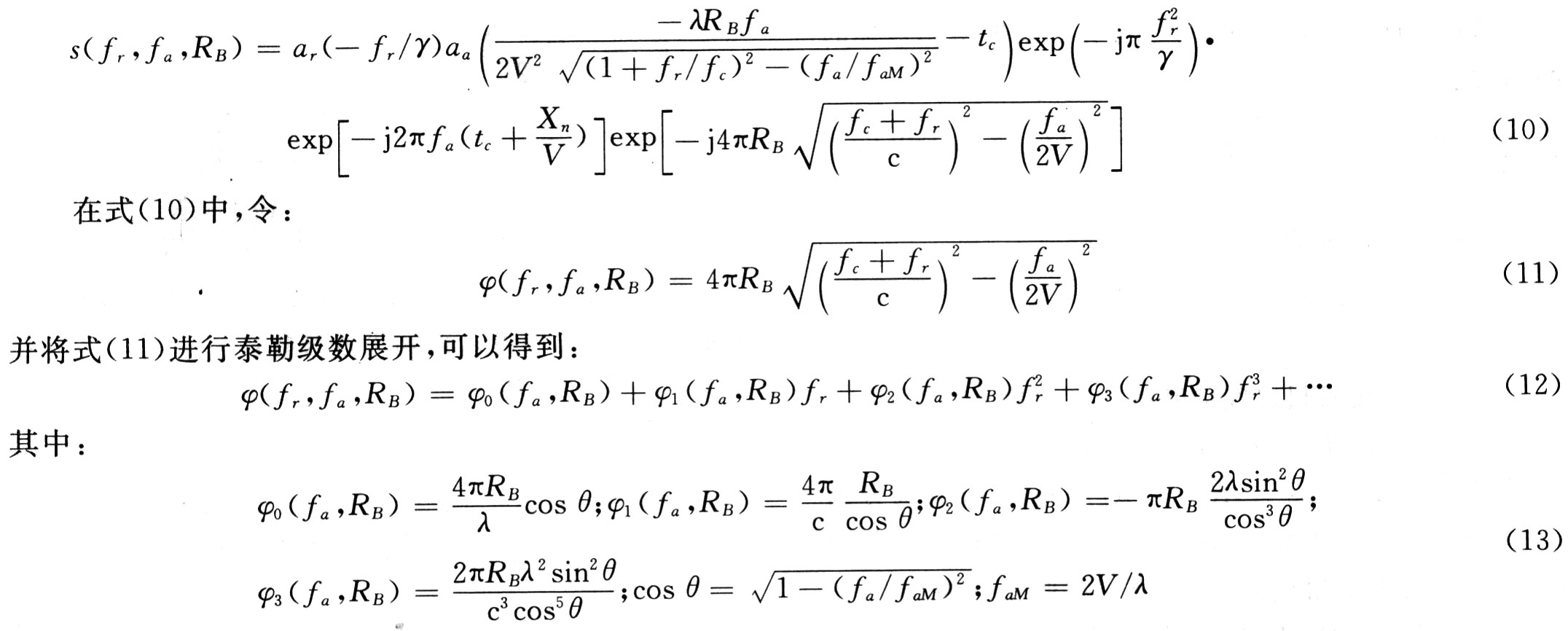
In the NCS algorithm, the influence of the phase term within three times is considered, and the influence of the higher-order phase term is ignored. The first four terms of the Taylor series expansion are approximated to obtain:

The result after the NCS operation is transformed into a two-dimensional frequency domain, and the RCMC and SRC terms that vary with distance are removed, and three coefficients can be obtained:
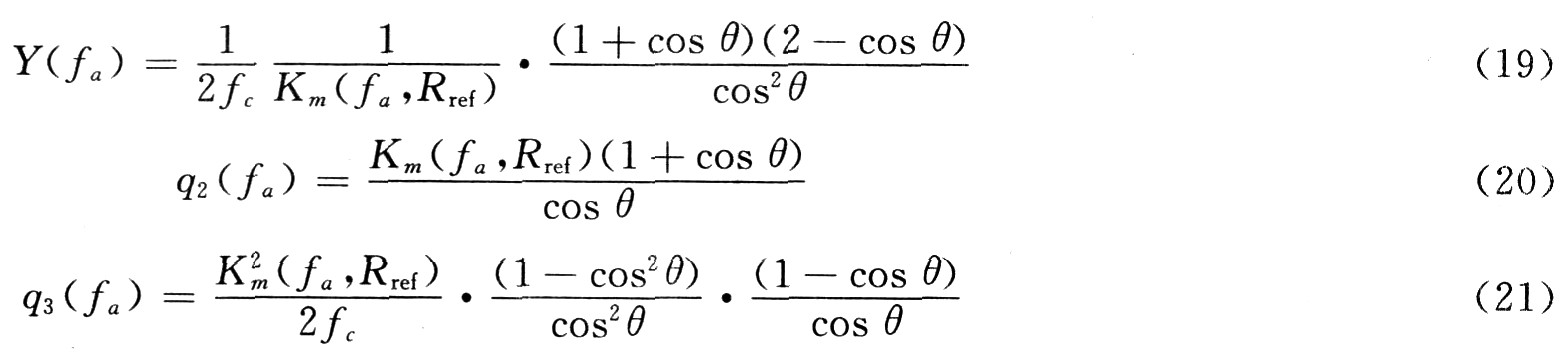
(5) Distance compression and bending correction After CS operation, the echo signal (only the phase term is considered at this time) can be expressed as:

The reference functions for distance compression and bending correction are:
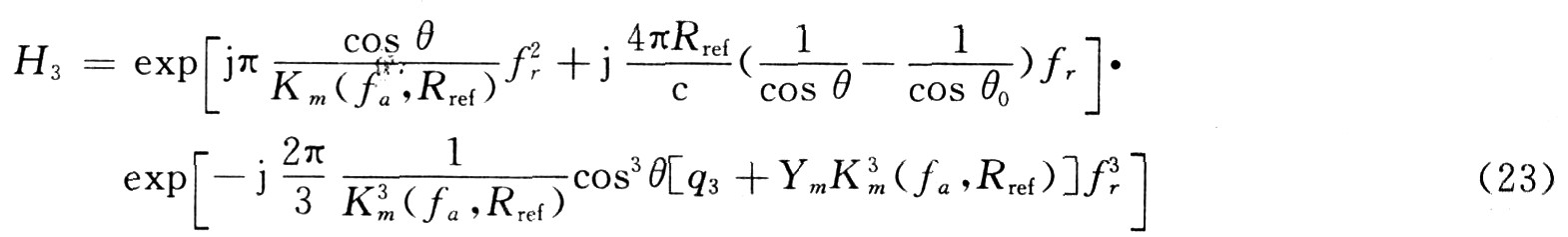
After distance compression and bending correction, the echo signal is transformed into the distance Doppler domain.
(6) Azimuth compression and residual phase compensation The azimuth compression and residual phase error compensation functions are shown in equation (24):
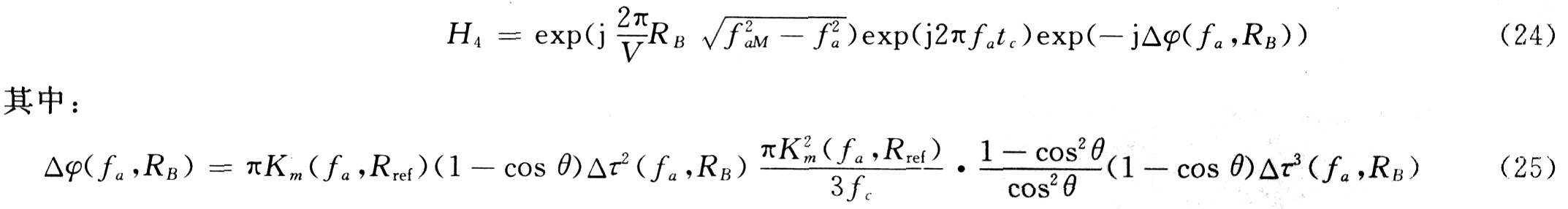
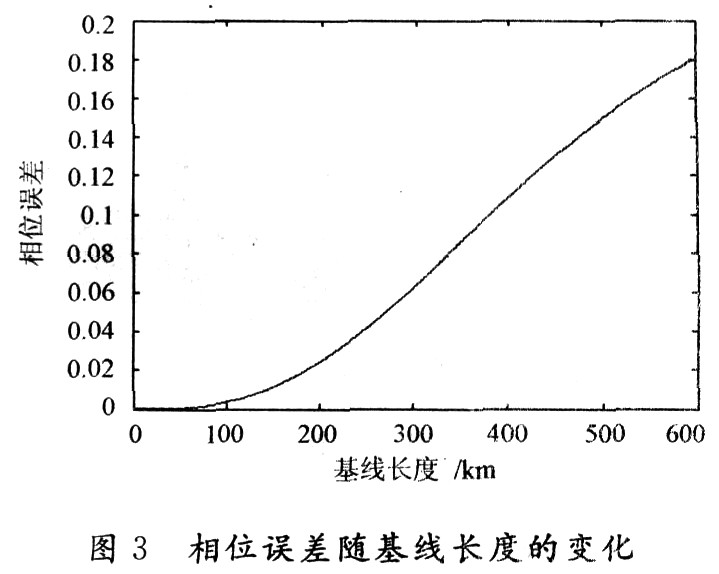
4 Error analysis (1) Change of phase error with baseline length Equivalent bistatic SAR to single-base SAR will produce a certain phase error, and the phase error also changes with the length of the baseline. The oblique angle of view of the fixed transmitter can be calculated to have different baseline lengths, which corresponds to the equivalent equivalent range, velocity, and oblique angle of view of the bistatic SAR equivalent to the monostatic SAR, which corresponds to different phases. Error, Figure 3 shows the phase error as a function of baseline length.
In Figure 3, the bistatic SAR is equivalent to the phase error generated by the single-base SAR increases with the increase of the baseline length. When the baseline length reaches 200 km, the phase error generated is still less than π / 8.
(2) Effective mapping band width The NCS algorithm takes into account the three-phase phase expansion of the phase Taylor series, which makes the phase error generated by the phase Taylor series approximation very small and will not be analyzed here. At the same time, the NCs algorithm considers the change of the frequency modulation with the distance, and reduces the phase error due to the frequency modulation approximation, so that the NCS can image the large mapping zone. Equation (26) is the phase error generated by the quadratic distance compression term in the NCS algorithm:
![]()
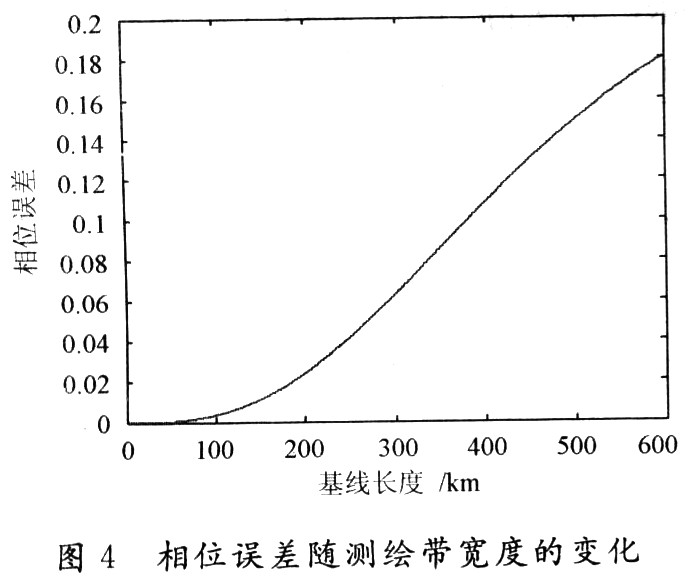
The width of the bistatic SAR mapping zone is mainly determined by the equivalent monostatic SAR. Figure 4 shows the variation of the phase error with the width of the mapping band. If π / 8 is used as the critical value of whether the phase error has any influence on the imaging quality, the effective mapping bandwidth can reach 200 km.
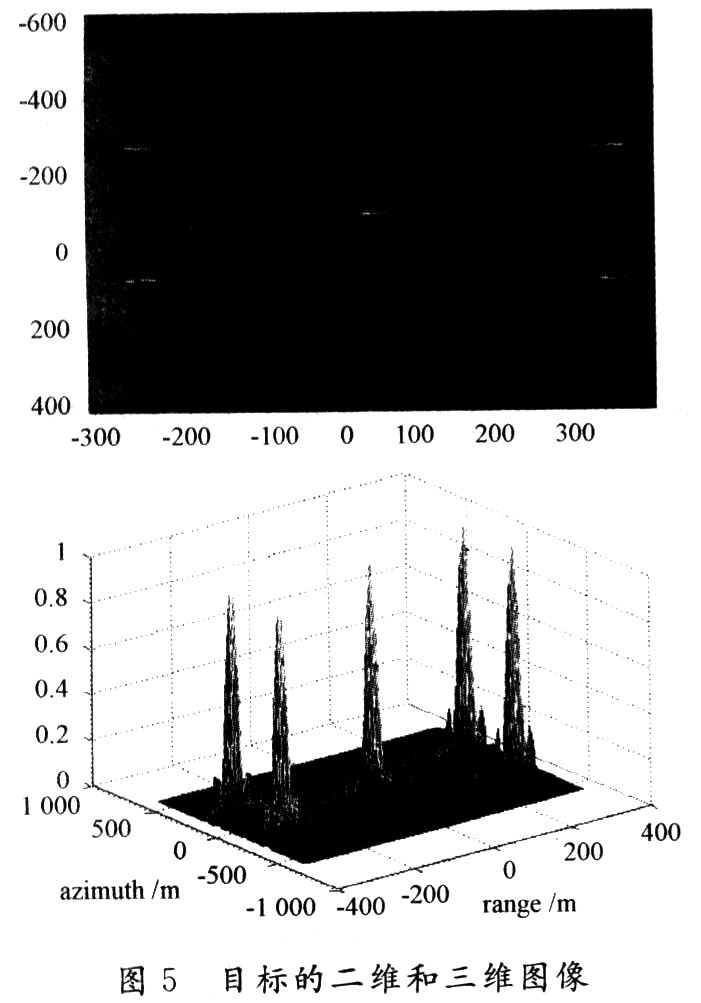
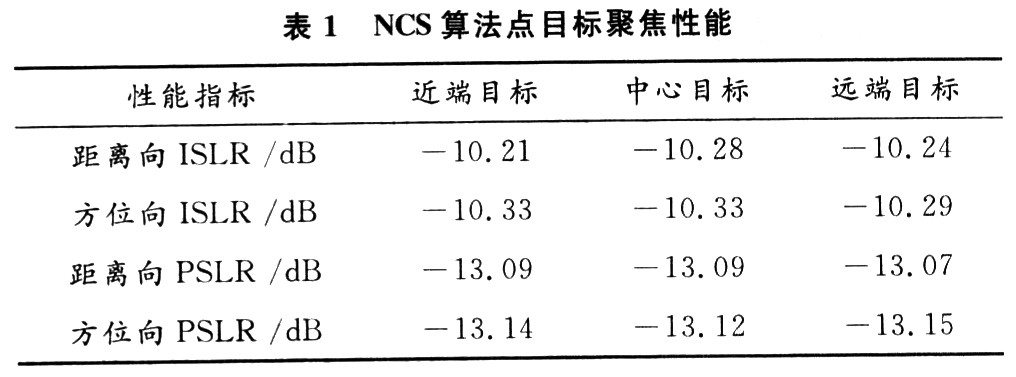
5 Simulation test In order to verify the equivalent single-base distance model, the applicability of bistatic SAR imaging based on GPS reflected signals in the case of a large oblique viewing angle, the above algorithm was verified by computer simulation, and the oblique viewing angle was set to 31. 4 °, the targets are (one 300, one 200), (one 300, 200), (0, O), (300, -200), (300, 200). Figure 5 shows the simulation scene settings and the two-dimensional and three-dimensional display of the simulation results. It can be seen that the equivalent single-base distance model can well approximate the true distance history of bistatic SAR. The linear CS algorithm is directly applied to bistatic SAR data, simplifying the imaging process of bistatic SAR. Table 1 shows the focusing performance of targets at different positions, where “PSLR†represents the peak sidelobe ratio and “ISLR†is the integrated sidelobe ratio in dB. The data in the table further proves the availability of the equivalent single-base distance model .
6 Conclusion In the orbital flight squint bistatic SAR, the CS algorithm is considered to be a more effective algorithm. In the case of a positive side view or a small slant angle of view, the Chirp Scaling algorithm has good focusing performance and wide practicality. However, the algorithm will not be able to focus well in the case of large surveying and large oblique viewing angles. Here, a method of replacing the bistatic distance history with an equivalent single-base distance model is proposed to solve the second-order distance model in the case of large oblique viewing angles. The problem of large approximation error, combined with the single-base non-linear CS algorithm, realizes high-precision imaging of GPS-based bistatic SAR in the case of large oblique viewing angles. Finally, it is simulated and verified by Matlab.
Filter Choke Inductor,power Filter Inductor,PCB mount Filter Inductor,UU Filter Inductor,Common Mode Choke Filter
IHUA INDUSTRIES CO.,LTD. , https://www.ihua-inductor.com