In the use of semiconductor devices, it is often necessary to understand and control the junction temperature. For a long time, the user of the device needs to know the junction temperature by using the thermal resistance value provided by the device manufacturer. By testing the temperature of the relevant point, the junction temperature is calculated according to the thermal resistance value. Everyone has followed this practice for decades. The LED industry has also followed this approach. However, the problems with this approach have rarely been noticed.
This paper uses simulation software to investigate the thermal resistance in measuring the junction temperature of semiconductor devices. These problems are undetectable if they are not visually generated by the results of simulation software calculations. Of course, if your mathematics ability is very strong, it is not impossible to manually solve the micro-powder equation to draw images such as isothermal surface, but the workload is huge and it takes a long time. With simulation software, it may take half an hour to get results. These problems can be very difficult if they are tested by experiments, such as getting isothermal conditions everywhere. For this reason, the improper use of the thermal resistance method to measure the junction temperature error has not been known.
This paper first introduces the basic theory of heat transfer and discusses it. The simulation is then used to verify the problem in question.
This paper proposes the concept of "intrinsic equivalent thermal resistance". It is also stated that only the intrinsic equivalent thermal resistance value can be provided to the customer as a characteristic parameter of the semiconductor device. And remind you that not all devices' intrinsic equivalent thermal resistance test points can be a practical test point.
It can be seen that the thermal resistance method is not a very practical method to measure the junction temperature. And the general equivalent thermal resistance value of the extrinsic thermal resistance temperature measurement point on the device is wrong for calculating the junction temperature. The error is not just a numerical difference, but an application of theoretical errors.
The content discussed in this article is mainly for the junction temperature measurement of semiconductor devices.
one
Introduction to the basic theory of heat transfer and discussion of problems
1 Introduction to basic theory
When examining heat transfer, heat convection, and heat radiation heat transfer separately, there are mathematical expressions for the following basic laws:
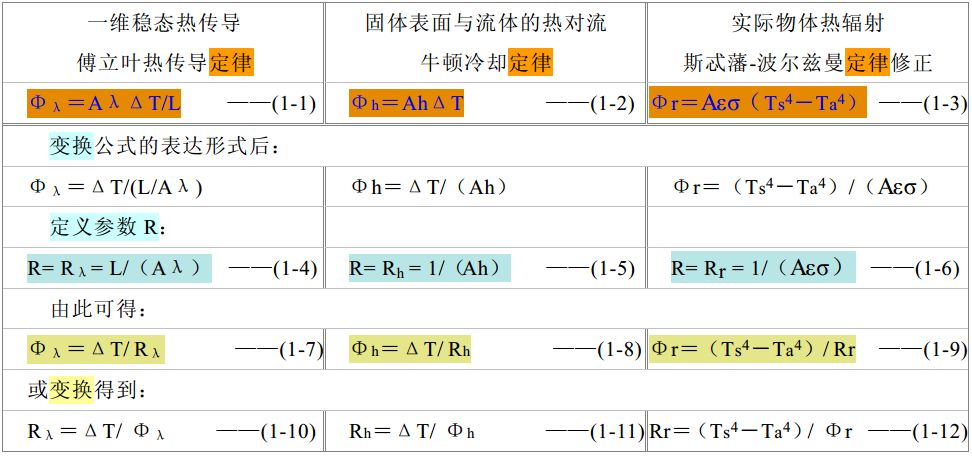
Reminder: Please readers should think and understand the ins and outs of the above formula.
Usually, without confusing and special emphasis, the parameters Φ and R indicate that the lower corners (λ, h, r) of conduction, convection and radiation are not required.
According to the common law of various transfer processes: the amount of transfer in the process = the power in the process / the resistance in the process, the parameter R is named thermal resistance.
For thermal radiation, the shape factor between objects is not considered here. After considering the shape factor of the object, the angle coefficient parameter must be added to formula (1-3). I won’t talk much about it here.
The basic theory introduced above, in practical applications, is often not able to simply use the above formula. The theory is often to extract the actual situation and find out the most basic rules. The actual situation is often the result of many different laws working together. Therefore, often on a macro scale, the above formula can only be applied to some special occasions. The actual heat transfer process is often three-dimensional. In many cases, to calculate the heat transfer condition, the heat transfer differential equation needs to be solved. In the formula of the differential equation, the parameter of thermal resistance is not used. Since they are not related to the thermal resistance parameters, they are not discussed in this article.
2 Discussion on the application of basic theory
The formula for the thermal resistance given in some standard data [1] [2] is:
R=ΔT/ Φ ——(1-13)
Where Φ usually refers to the power consumption of the device. (For LEDs, Φ should be electrical power minus optical power.)
Of course, in the data [1], his guiding ideology is that the heat of the chip is only transmitted in the package. If it is a heat transfer in a pure object, or a heat transfer between two isothermal surfaces that are completely in the fluid, using the concept of equivalent thermal resistance described in the next section, using equation (1-13) is not a problem. In fact, at the point on the surface of the package, the isothermal surface may not be completely within the surface of the package, but beyond the surface of the package. The formation of this isothermal surface is affected by the convection and radiation of the external structure and related surfaces. Especially after the influence of radiation, the formula (1-13) is no longer valid. Using equation (1-13) again is theoretically wrong.
Formula (1-13) is usually applied to the calculation of various heat transfer occasions. For example, let's take a look at the problem of this approach.
Assume that only the upper surface of the object is exposed to the air, and the other surfaces are insulated. And assume that the upper surface temperature is uniform. The heat flow Φ generated from the lower surface of the object propagates in a steady state through convection and radiation through the upper surface, and the total heat flow to the air is:
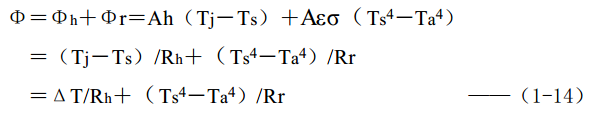
From the formula (1-14), a simple form similar to the formula (1-13) cannot be derived. That is to say, in the case where the radiant energy cannot be ignored, the formula (1-13) is not established.
3 intrinsic equivalent thermal resistance
The concept of intrinsic equivalent thermal resistance is introduced here.
To talk about the intrinsic equivalent thermal resistance, first introduce the concept of equivalent thermal resistance.
Equivalent thermal resistance: There are many thermal resistances in series and parallel between two isothermal surfaces. The overall result is replaced by a thermal resistance. This thermal resistance is called equivalent thermal resistance.
In general, the equivalent thermal resistance can be simply referred to as thermal resistance.
Intrinsic Equivalent Thermal Resistance: An isothermal surface of a device with an internal heat source reaches the boundary of the package, but does not exceed the boundary of the body. The equivalent thermal resistance between the isothermal surface and the isothermal surface of the internal heat source is called the intrinsic equivalent. Thermal resistance. It can be represented by the symbol Rb.
The difference between the equivalent thermal resistance and the intrinsic equivalent thermal resistance concept (see Figure 1):
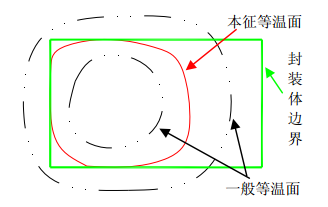
figure 1
The concept of equivalent thermal resistance applies to any two isothermal surfaces. The concept of intrinsic equivalent thermal resistance applies only to the case where an isothermal surface touches the boundary of the device body but does not exceed the boundary. Of course, the isothermal surface does not necessarily mean that the entire surface touches the boundary of the body, and may be a partial area or a point.
The concept of intrinsic equivalent thermal resistance can be applied to a package having a closed, hollow structure.
It can be said that the intrinsic isothermal surface is a special isothermal surface in the general isothermal surface. The intrinsic equivalent thermal resistance is a special equivalent thermal resistance.
Special note: The concept of intrinsic equivalent thermal resistance must understand the definition of its contents! Don't expect to be convinced that the equivalent thermal resistance of the isothermal surface at any point on the body heat source is the intrinsic equivalent thermal resistance.
The schematic diagram of Fig. 2 is used to illustrate the situation in which the equivalent thermal resistance changes after the structural system is changed. For the sake of convenience, Figure 2 only illustrates the thermal resistance of a particular direction (horizontal and vertical).
For System 1, it is assumed to be an axisymmetric heat dissipation structure, and System 2 does not have a symmetrical structure. It is assumed that the structure between the two points A1 and B1 does not change in the structural systems 1, 2 and serves as the location of the temperature measurement point.
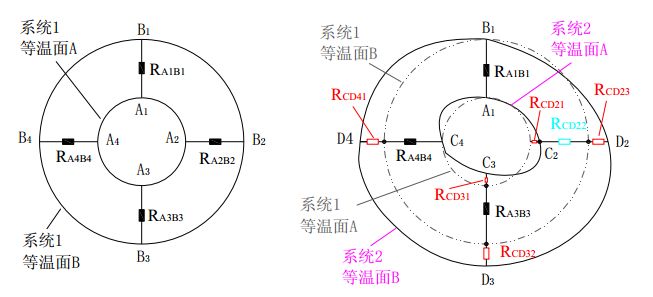
figure 2
For system 1, the equivalent thermal resistance of A and B faces is: R1=RA1B1//RA2B2//RA3B3//RA4B4 For system 2, the equivalent thermal resistance of A and B faces is: R2=RA1B1//RC2D2// RC3D3//RC4D4 where: RC2D2=RA2B2-RCD21+RCD23; RC3D3=RA3B3+RCD31+RCD32; RC4D4=RA4B4+RCD41 from above: R1 ≠R2
It can be seen from the above analysis that even in System 2, the position and structure of the A1-B1 point are the same as those in System 1, but the isothermal surface changes due to other structural changes, and the equivalent thermal resistance between the two points is also obtained. There have also been changes.
Since the intrinsic isothermal surface does not exceed the surface of the package, the heat transfer in the isothermal surface is independent of the convection and radiation conditions of the outer surface. The intrinsic equivalent thermal resistance is determined only by the parameters of the package itself. The intrinsic equivalent thermal resistance of a semiconductor device is generally only a conduction thermal resistance.
The conditions of the equivalent thermal resistance and the intrinsic equivalent thermal resistance can be clearly seen in the subsequent simulation results. Only the intrinsic equivalent thermal resistance can be used as a characteristic parameter of the device. The value obtained by the general equivalent thermal resistance of the device surface using the formula (1-13) has no practical significance.
Although the concept of intrinsic equivalent thermal resistance is introduced, it is sometimes not straightforward to find the temperature measurement point of the intrinsic equivalent thermal resistance. It is still more complicated to do manual calculations. In the past, due to the complexity of the calculation, almost no one calculated it very well, so it was not recognized how the application of the thermal resistance parameter was correct and how to use it was incorrect. Now you can use the simulation software to do related calculations. You can see the isothermal surface by the results of the software calculation, and you can see the isothermal surface at any point on the device changes with the external structure. Therefore, it can be well recognized that the thermal resistance value obtained by the incorrect temperature measurement point is not practical. Simulation software can be used to find the intrinsic isothermal surface of the device and thereby determine the test point for the intrinsic equivalent thermal resistance.
However, for some devices, there may be no ideal intrinsic equivalent thermal resistance temperature measurement points due to the package structure. For example, in a package like the 3528, the isothermal surface at the solder joint is far beyond the package body. Solder joints are not suitable as a temperature measurement point for examining the junction temperature of the LED.
This can be seen in the later simulation example. For some small packaged devices, the temperature test points of the intrinsic isothermal surface may not be applicable in actual use.
two
Looking at the calculation of thermal resistance by simulation
1 Simulation calculation of verification theory
1.1 Models and results of the simulation
The simulated models are the following two:
Model 1: A long strip of aluminum with dimensions: length x width x height = 1 mm x 1 mm x 40 mm. The model is placed vertically. The bottom surface is set as the heat source side. The heat source power is 0.004W. An insulated package is placed on the periphery, leaving only one of the upper surfaces as a heat dissipation surface. See Figure 3.
Model 2: The insulation package in Model 1 is removed, and other conditions are the same as Model 1. See Figure 4.
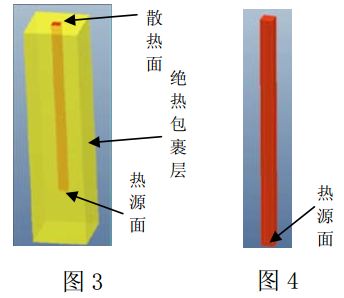
Simulation conditions: The thermal emissivity of the aluminum surface was 0.8. The thermal conductivity of aluminum is 201W/(m·K). The thermal conductivity of the thermal insulation layer is zero. The simulation was carried out using ambient temperatures of 20 ° C and 30 ° C, respectively.
The relevant data of the simulation results are shown in Table 1.

Description of the parameters in Table 1:
The heat transfer amount in Table 1 is the average value of the heat transfer amount of the upper surface (S point).
Since the cross-sectional area of ​​the model is 1, the following formula eliminates the area parameter A. Theoretical thermal resistance of one-dimensional heat conduction of the thermal conductor along the length direction: Rθ = L / (λS) The thermal resistance of the upper surface of the thermal conductor is simply applied by the formula (1-13): Rs = ΔT / Φ Φ refers to the total heat flux of the heat source.
The following is combined with the data in Table 1, through analysis, to see where many errors are.
1.2 Analysis of simulation results and related calculation methods
Analysis of Model 1:
In the case of insulated packages, heat can only be conducted in one direction of the aluminum strip, and the heat transfer of the aluminum strip can be considered as a one-dimensional heat transfer condition. At this point we can see that Rs is close to the theoretical value Rθ.
Analysis of Model 2:
For aluminum strips exposed to the air. Heat can dissipate heat from all sides. At this point we see that Rs is far from the Rθ value. This is because the heat is also transferred through the side of the aluminum strip, which is equivalent to a number of heat transfer paths in parallel with the top surface of the aluminum strip. The Rs value at this time is the result of many thermal resistances being connected in parallel. And it can be seen that changes in the ambient temperature will also cause changes in the Rs value.
Looking at the simulation results of the two models, the aluminum strip did not change, changing the structure outside the aluminum strip—with or without a thermal barrier.
The change in the external structure of the aluminum strip causes a change in the thermal resistance value calculated according to the formula (1-13) at the fixed position on the aluminum strip.
If the model 1 is not insulated, but the aluminum surface is changed, that is, the thermal emissivity of the surface is changed (can be changed by oxidation, paint, etc.), the result is still caused by the formula at the upper surface (1-13). The calculated thermal resistance values ​​are different.
1.3 The meaning of this simulation
From the results of the simulation comparison, it is known that the thermal resistance value from the top surface of the aluminum strip to the heat source end changes due to the change in the heat transfer condition of the side of the aluminum strip. The thermal resistance value obtained in this case is not versatile.
For any point on an actual non-one-dimensional heat transfer object, the thermal resistance value relative to the heat source point is often the equivalent value in parallel with other thermal resistance. It is not the conduction heat resistance of the line or the shortest distance between the heat source and the point. Since there is a parallel surface, there is energy transmitted by the radiation, which makes the formula (1-13) no longer valid. Even if a so-called thermal resistance value is forcibly calculated using the formula (1-13), the value can only express the case of the structure. The structure changes and the value is no longer meaningful.
2 Simulation of LED products
Take the LED of the chip package as an example. Usually the packaging factory will give the thermal resistance of the LED. The external temperature measurement point of the thermal resistance is generally the LED solder joint. However, the specific position of the solder joint is not indicated in the general specification. This is a problem for the practical application of the thermal resistance value because the LED heat sink and solder joint of some chip packages are integrated.
2.1 Simulation of LG 5630 packaged LEDs
This article discusses from two test points. The two test points are, one point is the bottom of the heat sink and directly below the center of the chip (point C), and the other point is the outer side of the electrode pad (point S). See Figure 5. The manual for the product states that the thermal resistance is the Junctiong to Solder Point between the solder joints. From Figure 5, the heat sink bottom and the electrode solder joint are solder joints that are electrically connected. Is the test point given in the manual C point or S point? As can be seen from the simulation results below, the thermal resistance values ​​of the two points to the PN junction are not equal.
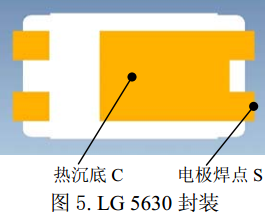
The LEDs are dissipated with different PCB copper layouts. Through simulation calculations, we examine the temperature, junction temperature and thermal resistance of the two temperature measurement points. Figures 6 and 7 show the results of two PCB layouts and simulation calculations, respectively. The power of the LED chip is 0.35W. The area of ​​the heat-dissipating copper foil is the same (the blue part in the figure. In order to save the drawing, it is not completely displayed).
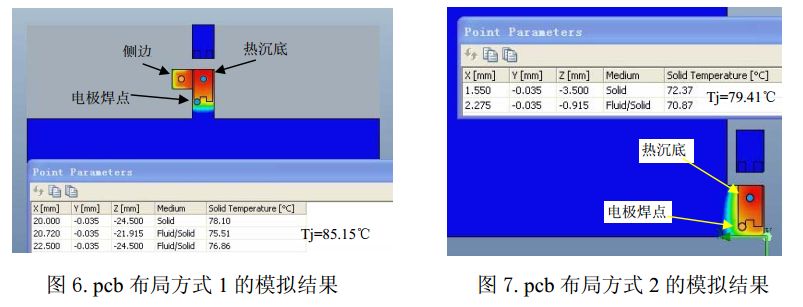
From the calculation results, the temperature difference between the heat sink bottom and the electrode pads is 2.7 ° C and 1.5 ° C under the two pcb layouts. From the point of view of the obvious temperature difference, it is necessary to calculate the junction temperature and not to select the temperature measurement point.
If the thermal resistance is calculated according to formula (1-13), let us calculate the thermal resistance of the two temperature measurement points to the PN junction.
For the structure of Figure 6, the thermal resistance of the heat sink bottom C point and the electrode joint S point to the PN junction are: RJC = (85.15 - 78.1) / 0.35 = 20.14 (K / W) RJS = (85.15 - 75.51) / 0.35 =27.54 (K/W)
For the structure of Figure 7, the thermal resistance of the heat sink bottom C point and the electrode solder joint S point to the PN junction are: RJC = (79.41 - 72.37) / 0.35 = 20.11 (K / W) RJS = (79.41 - 70.87) / 0.35 =24.4 (K/W)
Let's take a look at the isothermal surface. Figures 8 and 9 correspond to the isothermal surface conditions of Figures 6 and 7, respectively. It can be seen that for the LED of the LG5630 package, the isothermal surface of the C point just below the heat sink bottom chip does not substantially exceed the package body; and the isothermal surface at the S point of the solder joint has exceeded the package body.

It can be seen from the above settlement results that the equivalent thermal resistance value RJC of the isothermal surface does not exceed the temperature measurement point C of the package is not affected by the external heat transfer structure; and the isothermal surface exceeds the temperature measurement point S of the package, and its isothermal surface The equivalent thermal resistance value RJS is affected by the external heat transfer structure.
In the above two structures, we can confirm that the isothermal surface at point C is the intrinsic isothermal surface, and RJC is the intrinsic equivalent thermal resistance.
Comparing Figure 8 with Figure 9, it can be seen that for the isothermal surface of the heat sink bottom that does not exceed the boundary of the body, the isothermal surface shapes of the two structures are basically the same; and the isothermal surface at the solder joint exceeds the boundary of the device body, and the two are isothermal. The shape of the face is significantly different. Note that the isothermal surface shape at the solder joint is affected by the external structure of the device.
If the parameters of the device are to be characterized by parameters such as thermal resistance, then the concept of intrinsic equivalent thermal resistance should be used. The test point of the extrinsic equivalent thermal resistance is changed because the isothermal surface is changed by the external structure, and the calculated so-called thermal resistance value is not versatile, so it cannot be used as a characteristic parameter of the device.
In fact, the temperature points of the intrinsic isothermal surface of many semiconductor devices are on the outer surface of the heat sink directly below the chip. However, for a smaller device, the intrinsic equivalent thermal resistance value of the heat sink bottom directly below the chip is often not practical. Because the temperature cannot be measured here in actual use. For example, LEDs such as 5630, 5730, 2835, and 3014, after soldering to the PCB, cannot place a temperature probe at point C to test the temperature. Even if you place a temperature probe on the PCB under the LED, the size of the probe is relatively large compared to the size of the LED heat sink. Moreover, the probe metal has better thermal conductivity. Doing so actually destroys the original thermal condition of the LED. The results of this test are completely inaccurate.
Some manufacturers use the structure of the PCB copper-clad protruding at the bottom of the heat sink as the temperature measurement point of the thermal resistance, as shown in the "side" point of Figure 6. In fact, such a copper foil protrudes, and the position of the electrode pads is similar. Referring to the simulation results in Figure 6, the thermal resistance of the side temperature measurement point to the PN junction is:
R=(85.15-76.86)/0.35=23.69 (K/W)
Obviously, this thermal resistance value is obviously not equal to the intrinsic equivalent thermal resistance RJC value of the heat sink bottom. This temperature measurement point selection is wrong.
2.2 Simulation of 3528 Package LEDs
See Figure 10 for the isothermal surface of the 3528 LED. (The figure has hidden the PCB model)
As can be seen from Figure 10, the isothermal surface at the electrode pads is beyond the body of the device. For such encapsulated LEDs, there is no practical, suitable temperature measurement point for the intrinsic equivalent thermal resistance. Therefore, for such a packaged LED, the equivalent thermal resistance at the solder joint cannot be used as a characteristic parameter of the device. Because the equivalent thermal resistance of the solder joint changes with the external structure. For such devices, the junction temperature cannot be calculated using the thermal resistance method.

2.3 Simulation Summary in this Section
It can be seen from this simulation that for the extrinsic equivalent thermal resistance of the device, the thermal resistance value from the point to the isothermal surface of the heat source changes with the external structure of the device. Only the intrinsic equivalent thermal resistance of the device is not affected by the external structure, which may be a practical parameter.
The temperature test point of the intrinsic equivalent thermal resistance of the device needs to be determined by calculating the isothermal surface. That is, it is confirmed that the isothermal surface at which the point is located is the surface that contacts the body of the device but does not extend beyond the body.
three
in conclusion
1. For semiconductor devices, it is not possible to arbitrarily select a position on the surface as a thermal resistance test point for calculating the junction temperature. Only the position on the isothermal surface of the intrinsic equivalent thermal resistance can be used as the temperature test point for calculating the junction temperature. The extrinsic equivalent thermal resistance value is not universal and has no practical significance.
2. For the extrinsic temperature measurement point on the surface of the device, especially the temperature measurement point is selected outside the device body (such as PCB copper foil). From the formula (1-13) used in the calculation, it is theoretically Incorrect.
3. For smaller devices, even if there is an intrinsic isothermal surface on the surface of the package, it is often not a test point for practical applications. Such as LED 5630 package, 2835 package, 3014 package, and so on. Their intrinsic isothermal surfaces are in the center of the bottom of the device. Once the device is soldered to the PCB, the temperature cannot be tested at that location.
4. For some packaged devices, there may be no intrinsic isotherm available. For example, LEDs in the 3528 package. Therefore, such semiconductor devices cannot use the thermal resistance method to calculate the junction temperature.
References [1] GB/T 14862-1993 "Semiconductor integrated circuit package junction to case thermal resistance test method" [2] GB 3102.4-93 "The amount and unit of thermal"
Fiber Optic Cabinet,Fiber Cabinet,Fiber Distribution Cabinet,Outdoor Fiber Cabinet
Cixi Dani Plastic Products Co.,Ltd , https://www.dani-fiber-optic.com