Linear Programming Linear Programming is an optimization problem where the objective function and constraints are both linear. It is an important branch of research in operations research that is earlier, develops faster, is widely used, and is more mature. It is an aid to people's scientific management. A mathematical method, English abbreviation LP.
First, the business problem description: This is a simple linear programming problem, the specific requirements are as follows:
A company produces ammonia (NH3) and ammonium chloride (NH4CI). The company's daily processing capacity is 50 units of nitrogen (N), 180 units of ammonia (H), and 40 units of chlorine (CI). The profit of ammonia is The profit of 30$/unit/ammonium chloride is 40$/unit. How to determine the output of ammonia and ammonium chloride to maximize profits?
Second, understand and define this problem from a mathematical perspective:
Turning the above production problem into a mathematical problem, the establishment of a mathematical model generally has the following three steps:
1. Find the decision variable based on the factors that affect the goal to be achieved;
2. The objective function is determined by the functional relationship between the decision variable and its destination;
3. Determine the constraints to be satisfied by the decision variables from the constraints imposed by the decision variables.
Third, the OPL model to establish the steps
The following uses the OPL language to understand and define this problem. The OPL model is the process of finding the decision variable so that the decision variable satisfies the constraint condition and obtains the maximum value of the objective function. Here are a few steps to solve this problem:
1. Define the data variable for the problem,
For convenience, the data variables defined below are array variables. An array is a collection of ordered data. Each element in an array belongs to the same data type.
(1)Products stands for the name of the gas,
{string}Products = ...;
That is, an array of strings with an array named "Products" is defined, a one-dimensional array.
(2) Components represent the ingredients,
{string} Components = ...;
That is, an array of strings with an array name of "Components" is defined, a one-dimensional array.
(3) Demand represents the composition of each gas,
floatDemand[Products][Components] = ...;
That is, a floating-point array named "Demand", a two-dimensional array is defined.
(4) Profit represents the profit of the corresponding gas,
Float Profit[Products] =...;
That is, a floating-point array named "Profit" is defined, a one-dimensional array.
(5) Stock represents the daily processing capacity of this component,
Float Stock[Components] =...;
That is, a floating-point array named "Stock" is defined as a one-dimensional array.
2. The initialization of data;
After the data variable is defined, the initialization of the data is performed. The so-called initialization is to assign a value to the data variable. In the following, the data variable defined above is assigned in turn:
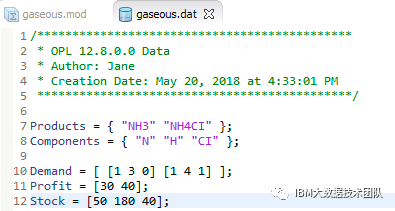
Products = { "NH3" "NH4CI"};
Components = { "N" "H" "CI"};
Demand = [[1 3 0] [1 4 1] ];
Profit = [30 40];
Stock = [50 180 40];
3. Define decision variables, data variables and decision variables are different, data variables are the names of specific data, such as the previously defined data variable "Products", which represents the name of the company's production gas, and decision variables are for mathematical models. The decision needed to make this issue is the output of each gas,
Dvar float+Production[Products];
Dvar (decision variable) is one of the most commonly used keywords for defining decision variables.
The decision variable with the variable name "Production" is defined here and represents the production of two gases. It is actually a floating-point array.
4. The definition of the objective function, ie, profit maximization, the objective function is a linear function of the decision variable,
Maximize
Sum( p in Products )
Profit[p] * Production[p];
5. For the setting of constraints, there are three components that have the limitation of daily processing capacity, and are implemented in a very concise way:
Subject to {
Forall( c in Components )
Ct:
Sum( p in Products )
Demand[p][c] * Production[p] <= Stock[c];
}
Fourth, use IBM ILOG CPLEX Optimization Studio 12.8 to solve this problem
The specific operation process of IBM ILOG CPLEX Optimization Studio 12.8 to solve this problem is as follows:
Open software interface, there are four commonly used windows, respectively, OPL project navigation window, edit window, problem browser window, output window;
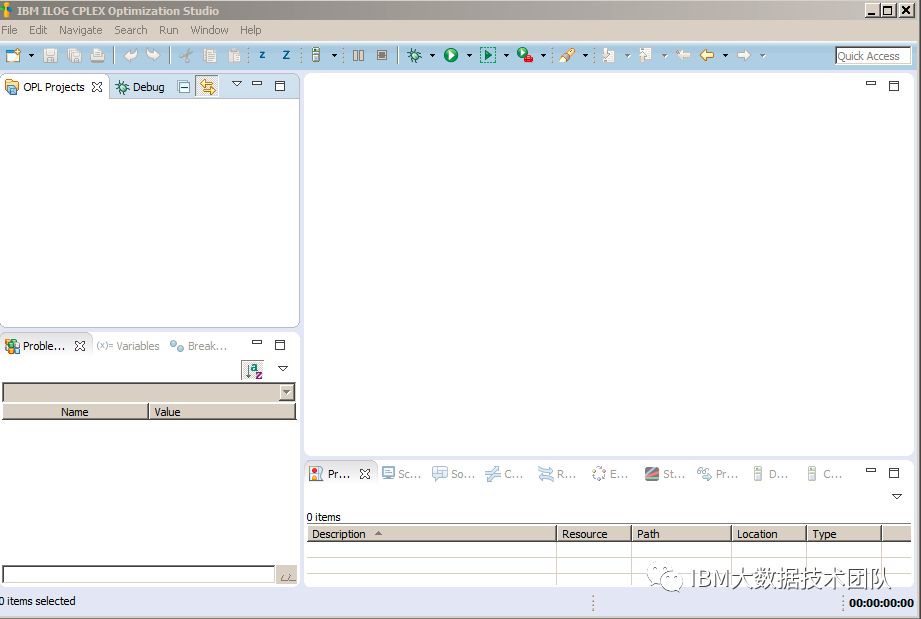
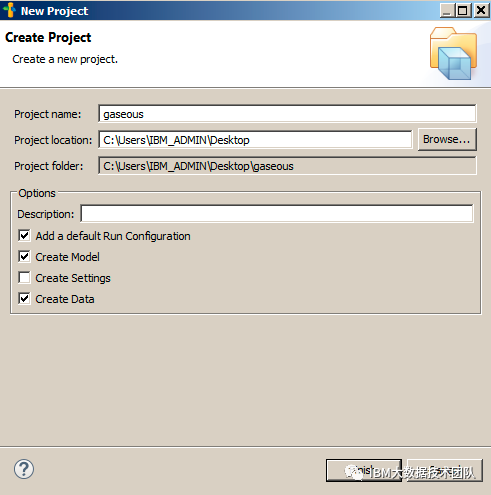
Create a new OPL project. The project name is "gaseous". Check the "Adda default Run Configuration", "CreateModel" and "CreateData". That is, the OPL project contains a model file and a data file.
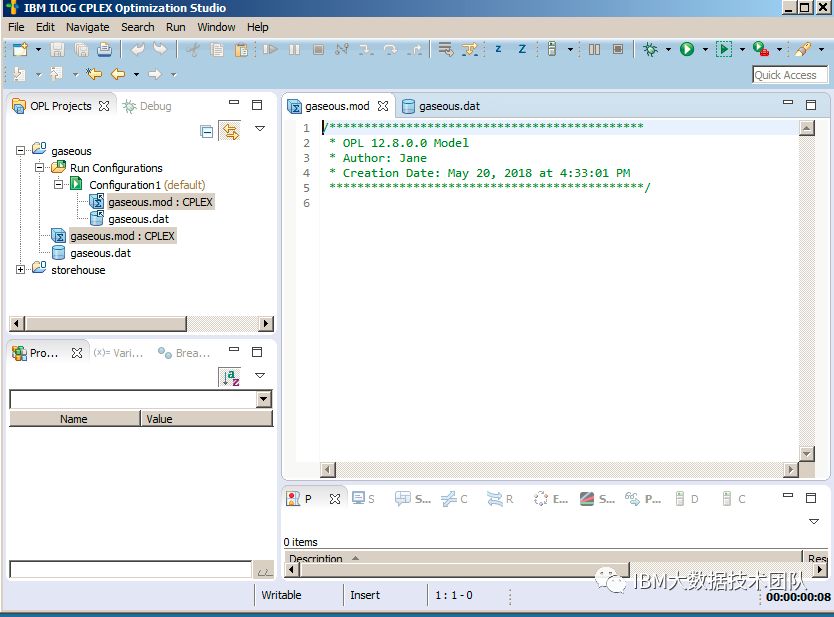
Edit the contents of the model file, the "gaseous.mod" file
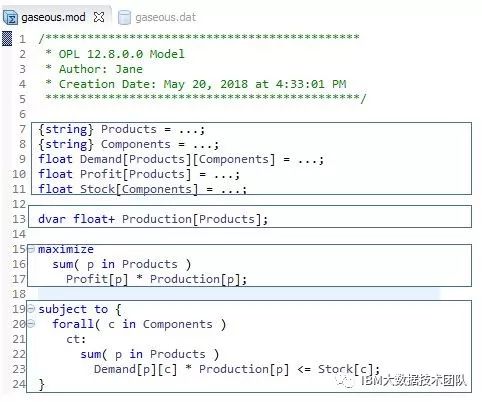
The content of this model file contains four parts:
(1) Define data variables;
(2) Define decision variables;
(3) Set the objective function;
(4) Set constraints;
Edit the contents of the data file, the "gaseous.dat" file
Then execute on "Configuration (default)":
Run Configuration, get the following output:
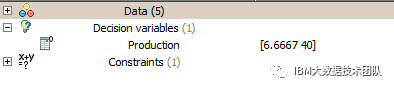
V. Business Interpretation
From the results of IBM ILOG CPLEX Optimization Studio 12.8, it can be seen that when ammonia production is 6.6667 units and ammonium chloride production is 40 units, the company gets the most profit and meets the processing capacity limit of each component on the day.
3V Lithium Carbon Fluoride Button Cells
3V Lithium Carbon Fluoride Button Cells use fluorocarbon material as the battery positive electrode. The fluorocarbon material has high thermal and chemical stability. It does not decompose at high temperature ≤600℃, and does not crystallize at low temperature. The battery operating temperature range can reach -40~125℃ ; Its chemical stability ensures the safety of the battery, so that the battery has a higher safety performance when short-circuit, collision, and extrusion, and has the characteristics of explosion-proof and spontaneous combustion. Our company uses self-developed electrolyte to make the battery life more than 10 years.
Our BR series button batteries are conventional high and low temperature resistant button batteries, and the working temperature is -40℃~+85℃
Accepts customized upgraded version of high and low temperature resistant button battery, working temperature is -40℃~ +125℃
Battery application range: It can be used in fields that have strict requirements for high and low temperatures and high energy density. For example, automobile tire pressure gauge (TPMS) battery, industrial control motherboard battery, computer motherboard battery, smart instrument battery, oil field drilling platform emergency equipment power supply, marine life-saving flasher, implantable medical battery, etc.
3V Lithium Carbon Fluoride Button Cells,Long Lasting Coin Battery For Watches,Lithium Coin Batteries For Household,3V Li-(Cfx)N Button Battery
Shandong Huachuang Times Optoelectronics Technology Co., Ltd. , https://www.dadncell.com